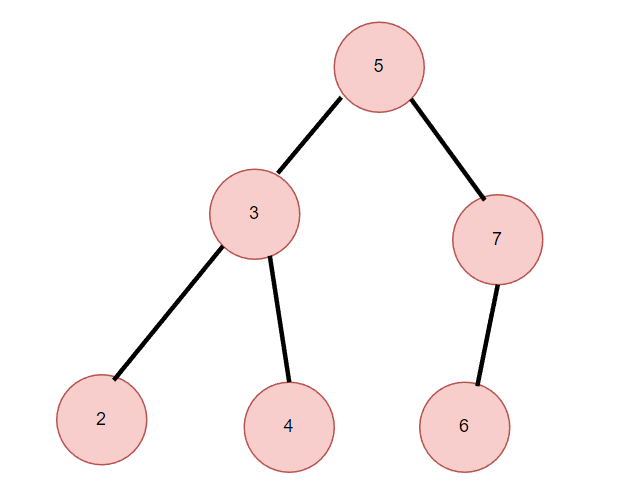
二叉搜索树(Binary Search Tree,BST)是一种特殊的二叉树,具有以下性质:
- 对于任意节点 n,其左子树中所有节点的值均小于节点 n 的值。
- 对于任意节点 n,其右子树中所有节点的值均大于节点 n 的值。
- 左子树和右子树也分别为二叉搜索树。
先创建一个BSTTree类
public class BSTTree {
BSTNode root; // 根节点
static class BSTNode {
int key;
Object value;
BSTNode left;
BSTNode right;
public BSTNode(int key) {
this.key = key;
}
public BSTNode(int key, Object value) {
this.key = key;
this.value = value;
}
public BSTNode(int key, Object value, BSTNode left, BSTNode right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
}在二叉搜索树中,对于给定值 x,可以通过以下方式在树中查找该值:
- 从根节点开始,若根节点为空,则返回 null;
- 若当前节点的值等于 x,则返回当前节点;
- 若 x 小于当前节点的值,则在左子树中继续查找;
- 若 x 大于当前节点的值,则在右子树中继续查找。
public Object get(int key) {
BSTNode node = root;
while (node != null) {
if (key < node.key) {
node = node.left;
} else if (node.key < key) {
node = node.right;
} else {
return node.value;
}
}
return null;
}
查找最小关键字对应值和最大关键字对应值。通过不断向左子树或右子树移动,直到找到最左侧或最右侧的节点,来找到最小值和最大值。
/**
* 查找最小关键字对应值
* @return 关键字对应的值
*/
public Object min() {
return min(root);
}
private Object min(BSTNode node) {
if (node == null) {
return null;
}
BSTNode p = node;
while (p.left != null) {
p = p.left;
}
return p.value;
}
/**
* 查找最大关键字对应值
* @return 关键字对应的值
*/
public Object max() {
return max(root);
}
private Object max(BSTNode node) {
if (node == null) {
return null;
}
BSTNode p = node;
while (p.right != null) {
p = p.right;
}
return p.value;
}
存储关键字和对应值,对于插入操作,需要按照上述查找规则找到合适的位置插入新节点,并保持二叉搜索树的性质不变。
public void put(int key, Object value) {
BSTNode node = root;
BSTNode parent = null;
while (node != null) {
parent = node;
if (key < node.key) {
node = node.left;
} else if (node.key < key) {
node = node.right;
} else {
node.value = value;
return;
}
}
if (parent == null){
root = new BSTNode(key,value);
return;
}
if (key < parent.key){
parent.left = new BSTNode(key,value);
}else {
parent.right = new BSTNode(key,value);
}
}
在二叉搜索树中,节点的“前任”指的是比当前节点小且值最接近当前节点值的节点。要找到一个节点的前任,步骤如下:
- 如果当前节点有左子节点,则前任节点是其左子树中值最大的节点,即左子树中一直向右走直到最右侧的节点。
- 如果当前节点没有左子节点,那么需要向上追溯直到找到第一个比当前节点小的祖先节点,或离它最近的祖先自从左而来,该祖先节点就是当前节点的前任。
public Object predecessor(int key) {
BSTNode p = root;
BSTNode ancestorFromLeft = null;
while (p != null) {
if (key < p.key) {
p = p.left;
} else if (p.key < key) {
ancestorFromLeft = p;
p = p.right;
} else {
break;
}
}
// 没找到节点
if (p == null) {
return null;
}
// 找到节点 情况1:节点有左子树,此时前任就是左子树的最大值
if (p.left != null) {
return max(p.left);
}
// 找到节点 情况2:节点没有左子树,若离它最近的、自左而来的祖先就是前任
return ancestorFromLeft != null ?
ancestorFromLeft.value : null;
}
在二叉搜索树中,节点的后任指的是比当前节点大且值最接近当前节点值的节点。要找到一个节点的后任,步骤如下:
- 如果当前节点有右子节点,则后任节点是其右子树中值最小的节点,即右子树中一直向左走直到最左侧的节点。
- 如果当前节点没有右子节点,那么需要向上追溯直到找到第一个比当前节点大的祖先节点或离它最近的祖先自从右而来,该祖先节点就是当前节点的后任。
public Object successor(int key) {
BSTNode p = root;
BSTNode ancestorFromRight = null;
while (p != null) {
if (key < p.key) {
ancestorFromRight = p;
p = p.left;
} else if (p.key < key) {
p = p.right;
} else {
break;
}
}
// 没找到节点
if (p == null) {
return null;
}
// 找到节点 情况1:节点有右子树,此时后任就是右子树的最小值
if (p.right != null) {
return min(p.right);
}
// 找到节点 情况2:节点没有右子树,若离它最近的、自右而来的祖先就是后任
return ancestorFromRight != null ?
ancestorFromRight.value : null;
}
删除操作稍复杂一些,分为三种情况处理:
- 若待删除节点没有子节点,直接删除该节点;
- 若待删除节点只有一个子节点,将其子节点替换为待删除节点;
- 若待删除节点有两个子节点,则找到其右子树中最小节点或左子树中最大节点来替换待删除节点,并删除该最小节点或最大节点。(代码使用右子树中最小节点)
public Object remove(int key) {
BSTNode p = root;
BSTNode parent = null;
while (p != null) {
if (key < p.key) {
parent = p;
p = p.left;
} else if (p.key < key) {
parent = p;
p = p.right;
} else {
break;
}
}
if (p == null) {
return null;
}
// 删除操作
if (p.left == null) {
shift(parent, p, p.right); // 情况2
} else if (p.right == null) {
shift(parent, p, p.left); // 情况2
} else {
// 情况3
// 3.1 被删除节点找后继
BSTNode s = p.right;
BSTNode sParent = p; // 后继父亲
while (s.left != null) {
sParent = s;
s = s.left;
}
// 后继节点即为 s
if (sParent != p) { // 不相邻
// 3.2 删除和后继不相邻, 处理后继的后事
shift(sParent, s, s.right); // 不可能有左孩子,否则不是后继节点
s.right = p.right;
}
// 3.3 后继取代被删除节点
shift(parent, p, s);
s.left = p.left;
}
return p.value;
}
/**
* 托孤方法
* @param parent 被删除节点的父亲
* @param deleted 被删除节点
* @param child 被顶上去的节点
*/
private void shift(BSTNode parent, BSTNode deleted, BSTNode child) {
if (parent == null) {
root = child;
} else if (deleted == parent.left) {
parent.left = child;
} else {
parent.right = child;
}
}
查找所有小于给定 key 值的节点值的操作。它使用迭代的方式进行中序遍历,从小到大地访问节点,并将小于给定 key 的节点值添加到结果列表中。
先沿着左子树一直向下遍历,直到最左侧的节点,遇到小于给定 key 值的节点值就加入栈。
// 找 < key 的所有 value
public List<Object> less(int key) { // key=6
ArrayList<Object> result = new ArrayList<>();
BSTNode p = root;
LinkedList<BSTNode> stack = new LinkedList<>();
while (p != null || !stack.isEmpty()) {
if (p != null) {
stack.push(p);
p = p.left;
} else {
BSTNode pop = stack.pop();
// 处理值
if (pop.key < key) {
result.add(pop.value);
} else {
break;
}
p = pop.right;
}
}
return result;
}
在二叉搜索树中查找所有大于给定 key 值的节点值的操作。它使用迭代的方式进行反向中序遍历,从大到小地访问节点,并将大于给定 key 的节点值添加到结果列表中。
先沿着右子树一直向下遍历,直到最右侧的节点,遇到大于给定 key 的节点就加入栈。
// 找 > key 的所有 value
public List<Object> greater(int key) {
ArrayList<Object> result = new ArrayList<>();
BSTNode p = root;
LinkedList<BSTNode> stack = new LinkedList<>();
while (p != null || !stack.isEmpty()) {
if (p != null) {
stack.push(p);
p = p.right;
} else {
BSTNode pop = stack.pop();
// 处理值
if (pop.key > key) {
result.add(pop.value);
} else {
break;
}
p = pop.left;
}
}
return result;
}
查找介于 key1 和 key2 之间的所有节点值的操作。其主要逻辑是利用迭代的方式进行中序遍历,并在遍历过程中判断节点的值是否在指定的范围内,然后将符合条件的节点值添加到结果列表中。
在整个遍历过程中,对于每个节点,都会先将其左子节点依次入栈,然后处理栈顶节点,最后转向其右子节点。这样可以确保按照从小到大的顺序依次访问节点,同时通过比较节点的值和给定的范围来决定是否将节点值加入栈。
// 找 >= key1 且 <= key2 的所有值
public List<Object> between(int key1, int key2) {
ArrayList<Object> result = new ArrayList<>();
BSTNode p = root;
LinkedList<BSTNode> stack = new LinkedList<>();
while (p != null || !stack.isEmpty()) {
if (p != null) {
stack.push(p);
p = p.left;
} else {
BSTNode pop = stack.pop();
// 处理值
if (pop.key >= key1 && pop.key <= key2) {
result.add(pop.value);
} else if (pop.key > key2) {
break;
}
p = pop.right;
}
}
return result;
}
参考