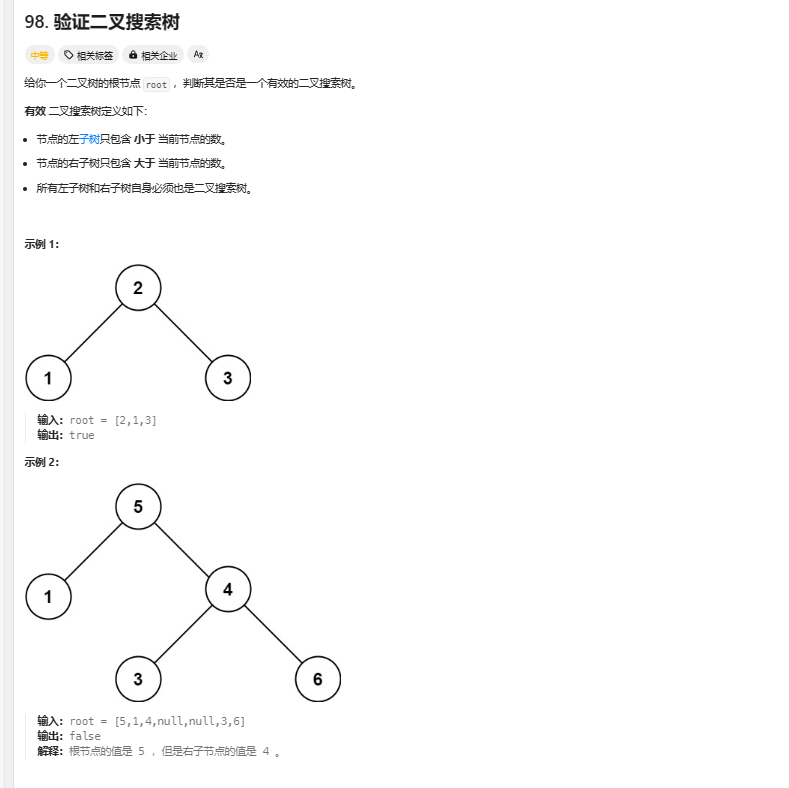
1.验证二叉搜索树

解法一 中序遍历非递归实现 1ms
public boolean isValidBST(TreeNode node) {
TreeNode p = node;
LinkedList<TreeNode> stack = new LinkedList<>();
long prev = Long.MIN_VALUE; // 代表上一个值
while (p != null || !stack.isEmpty()) {
if (p != null) {
stack.push(p);
p = p.left;
} else {
TreeNode pop = stack.pop();
// 处理值
// System.out.println("compare:" + prev + " " + pop.val);
if (prev >= pop.val) {
return false;
}
prev = pop.val;
p = pop.right;
}
}
return true;
}
中序遍历递归实现(全局变量记录 prev) 0ms
// 解法2. 中序遍历递归实现(全局变量记录 prev) 0ms
long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode node) {
if (node == null) {
return true;
}
boolean a = isValidBST(node.left);
if (!a) {
return false;
}
if (prev >= node.val) {
return false;
}
prev = node.val;
return isValidBST(node.right);
}
中序遍历递归实现(局部变量记录 prev,方法内的局部变量变化无效,所以使用对象) 0ms
public boolean isValidBST(TreeNode node) {
return doValid3(node, new AtomicLong(Long.MIN_VALUE));
}
private boolean doValid3(TreeNode node, AtomicLong prev) {
if (node == null) {
return true;
}
boolean a = doValid3(node.left, prev);
if (!a) {
return false;
}
if (prev.get() >= node.val) {
return false;
}
prev.set(node.val);
return doValid3(node.right, prev);
}
上下限递归实现 0ms
doValid4,接受三个参数:当前节点 node、当前节点允许的最小值 min、当前节点允许的最大值 max。递归地对左子树和右子树进行验证,更新相应的上下限:对于左子树,更新最大值为当前节点的值;对于右子树,更新最小值为当前节点的值。
public boolean isValidBST(TreeNode node) {
return doValid4(node, Long.MIN_VALUE, Long.MAX_VALUE);
}
private boolean doValid4(TreeNode node, long min, long max){
if (node == null) {
return true;
}
if (node.val <= min || node.val >= max) {
return false;
}
return doValid4(node.left, min, node.val) && doValid4(node.right, node.val, max);
}
2.二叉搜索树的范围和
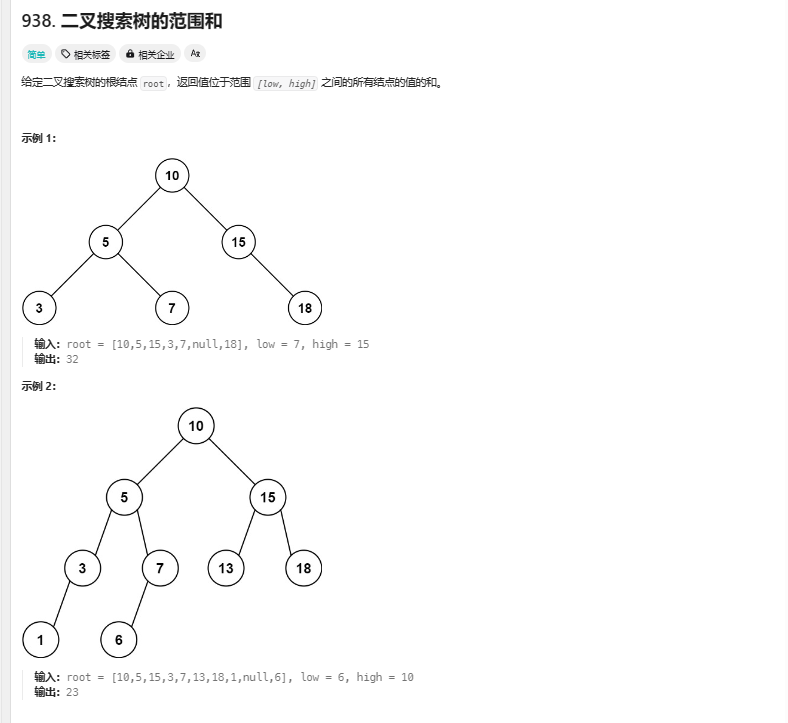

中序遍历非递归实现 4ms
public int rangeSumBST1(TreeNode node, int low, int high) {
TreeNode p = node;
LinkedList<TreeNode> stack = new LinkedList<>();
int sum = 0;
while(p != null || !stack.isEmpty()) {
if (p != null) {
stack.push(p);
p = p.left;
} else {
TreeNode pop = stack.pop();
// 处理值
if (pop.val > high) {
break;
}
if (pop.val >= low) {
sum += pop.val;
}
p = pop.right;
}
}
return sum;
}
上下限递归 0ms
public int rangeSumBST(TreeNode node, int low, int high) {
if (node == null) {
return 0;
}
if (node.val < low) {
return rangeSumBST(node.right, low, high);
}
if (node.val > high) {
return rangeSumBST(node.left, low, high);
}
// 在范围内
return node.val + rangeSumBST(node.left, low, high) + rangeSumBST(node.right, low, high);
}
3.前序遍历构造二叉搜索树
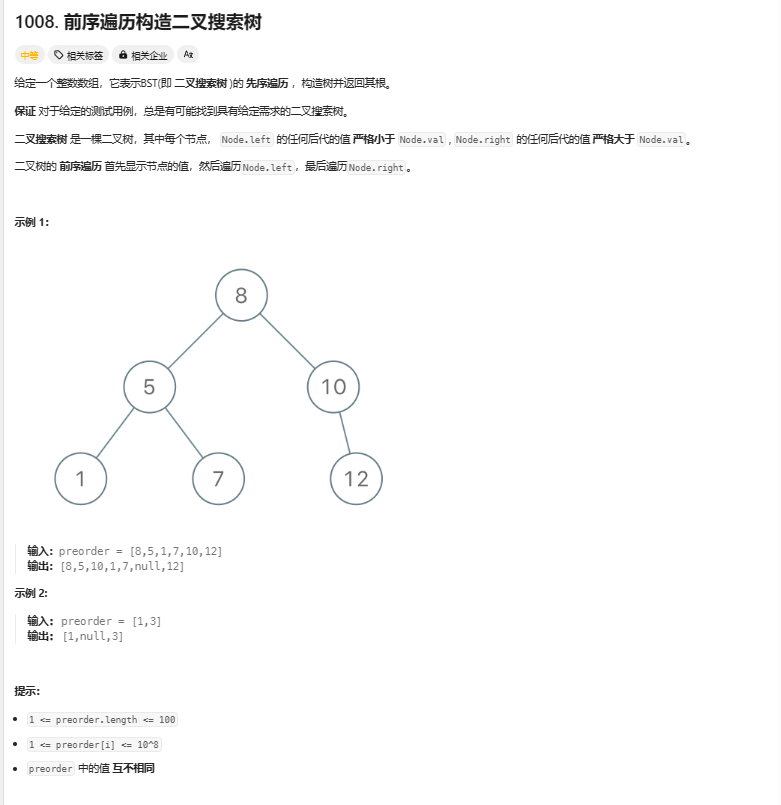
insert 方法是一个递归方法,用于将给定的值 val 插入到以 node 为根节点的二叉搜索树中。如果当前节点为空(即 node == null),则直接创建一个新节点并返回。如果 val 小于当前节点的值,则递归地将 val 插入到左子树中;如果 val 大于当前节点的值,则递归地将 val 插入到右子树中。最后返回当前节点 node。
最后返回构建好的 BST 的根节点 root。
public TreeNode bstFromPreorder(int[] preorder) {
TreeNode root = insert(null, preorder[0]);
for (int i = 1; i < preorder.length; i++) {
insert(root, preorder[i]);
}
return root;
}
private TreeNode insert(TreeNode node, int val) {
if (node == null) {
return new TreeNode(val);
}
if(val < node.val) {
node.left = insert(node.left, val);
} else if(node.val < val){
node.right = insert(node.right, val);
}
return node;
}
使用上限法(最优)构建二叉搜索树,使用了一个成员变量 index 来追踪前序遍历数组的当前位置,并根据上限值来确定节点的位置。在每次递归调用时,我们将当前值与上限值进行比较,以决定是否继续构建左子树或右子树。
private int index = 0;
public TreeNode bstFromPreorder(int[] preorder) {
return bstFromPreorder(preorder, Integer.MAX_VALUE);
}
private TreeNode bstFromPreorder(int[] preorder, int upper) {
if (index == preorder.length || preorder[index] > upper) {
return null;
}
TreeNode root = new TreeNode(preorder[index++]);
root.left = bstFromPreorder(preorder, root.val);
root.right = bstFromPreorder(preorder, upper);
return root;
}如果当前位置超过数组长度或者当前节点的值大于上限值,那么返回 null。否则,创建一个节点,并递增 index,然后递归构建左子树和右子树,分别将当前节点的值作为左子树的上限值。
使用分治法构建二叉搜索树时,通过递归地将问题分解成更小的子问题,然后将子问题的解合并起来得到最终的结果。
public TreeNode bstFromPreorder(int[] preorder) {
return constructBST(preorder, 0, preorder.length - 1);
}
private TreeNode constructBST(int[] preorder, int start, int end) {
if (start > end) {
return null;
}
TreeNode root = new TreeNode(preorder[start]);
int i;
for (i = start + 1; i <= end; i++) {
if (preorder[i] > root.val) {
break;
}
}
root.left = constructBST(preorder, start + 1, i - 1);
root.right = constructBST(preorder, i, end);
return root;
}
4.二叉搜索树的最近公共祖先

使用 while 循环来不断迭代找到最近公共祖先。
- 循环条件是:当节点 p 和节点 q 都在当前节点 a 的同一侧时,继续循环。
- 在循环中,通过比较节点 p 和节点 q 的值与当前节点 a 的值,来确定它们是否在同一侧。如果都小于当前节点的值或者都大于当前节点的值,则它们在同一侧。
- 根据节点 p 和节点 q 的值与当前节点 a 的值的比较结果,更新当前节点 a 为其左子节点或右子节点,以便继续向下搜索。
- 当节点 p 和节点 q 不在同一侧时,循环结束,返回当前节点 a,即为节点 p 和节点 q 的最近公共祖先。
代码如下
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
TreeNode a = root;
while (p.val < a.val && q.val < a.val || a.val < p.val && a.val < q.val) { // 在同一侧
if (p.val < a.val) {
a = a.left;
} else {
a = a.right;
}
}
return a;
}
参考
1008. 前序遍历构造二叉搜索树 – 力扣(LeetCode)