Huffman编码是一种基于字符出现频率的无损数据压缩算法。它通过构建一个最优前缀编码树来实现压缩，使得出现频率高的字符拥有较短的编码，而出现频率低的字符拥有较长的编码。

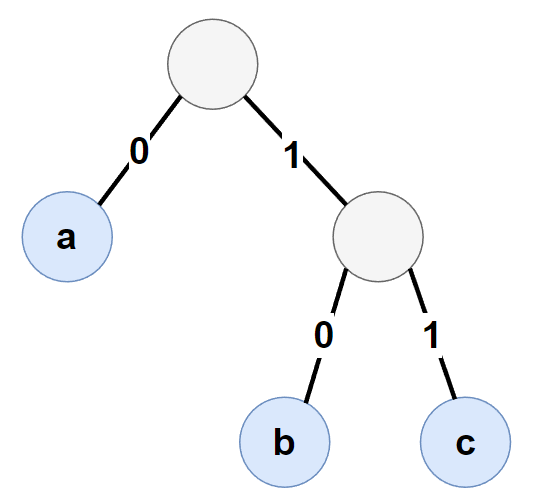
在构建Huffman树的过程中，会将频次较小字符路径尽可能的短，频次较大的字符反之，以此构建出一个最优的前缀编码树。

代码：

package com.dreams.Tree;

import java.util.Comparator;
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;

/**
 * Huffman 树以及编解码
 */
public class HuffmanTree {

    /*
        Huffman 树的构建过程
        1. 将统计了出现频率的字符，放入优先级队列
        2. 每次出队两个频次最低的元素，给它俩找个爹
        3. 把爹重新放入队列，重复 2~3
        4. 当队列只剩一个元素时，Huffman 树构建完成
     */

    static class Node {
        Character ch; // 字符
        int freq;     // 频次
        Node left;
        Node right;
        String code;  // 编码

        public Node(Character ch) {
            this.ch = ch;
        }

        public Node(int freq, Node left, Node right) {
            this.freq = freq;
            this.left = left;
            this.right = right;
        }

        int freq() {
            return freq;
        }

        boolean isLeaf() {
            return left == null;
        }

        @Override
        public String toString() {
            return "Node{" +
                    "ch=" + ch +
                    ", freq=" + freq +
                    '}';
        }
    }

    String str;
    Map<Character, Node> map = new HashMap<>();
    Node root;
}

在哈夫曼树添加属性

package com.dreams.Tree;

import java.util.Comparator;
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;

/**
 * Huffman 树以及编解码
 */
public class HuffmanTree {

    /*
        Huffman 树的构建过程
        1. 将统计了出现频率的字符，放入优先级队列
        2. 每次出队两个频次最低的元素，给它俩找个爹
        3. 把爹重新放入队列，重复 2~3
        4. 当队列只剩一个元素时，Huffman 树构建完成
     */

    static class Node {
        //......
    }

    String str;
    Map<Character, Node> map = new HashMap<>();
    Node root;
}

构造方法：

public HuffmanTree(String str) {
    this.str = str;
    // 功能1：统计频率
    char[] chars = str.toCharArray();
    for (char c : chars) {
        Node node = map.computeIfAbsent(c, Node::new);
        node.freq++;
    }
    // 功能2: 构造树
    PriorityQueue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(Node::freq));
    queue.addAll(map.values());
    while (queue.size() >= 2) {
        Node x = queue.poll();
        Node y = queue.poll();
        int freq = x.freq + y.freq;
        queue.offer(new Node(freq, x, y));
    }
    root = queue.poll();
    // 功能3：计算每个字符的编码, 功能4：字符串编码后占用 bits
    int sum = dfs(root, new StringBuilder());
    for (Node node : map.values()) {
        System.out.println(node + " " + node.code);
    }
    System.out.println("总共会占用 bits:" + sum);
}

计算每个字符的编码

private int dfs(Node node, StringBuilder code) {
    int sum = 0;
    if (node.isLeaf()) {
        node.code = code.toString();
        sum = node.freq * code.length();
    } else {
        sum += dfs(node.left, code.append("0"));
        sum += dfs(node.right, code.append("1"));
    }
    if (code.length() > 0) {
        code.deleteCharAt(code.length() - 1);
    }
    return sum;
}

编码方法

public String encode() {
    char[] chars = str.toCharArray();
    StringBuilder sb = new StringBuilder();
    for (char c : chars) {
        sb.append(map.get(c).code);
    }
    return sb.toString();
}

解码方法

// 解码
public String decode(String str) {
    /*
        从根节点，寻找数字对应的字符
            数字是 0 向左走
            数字是 1 向右走
            如果没走到头，每走一步数字的索引 i++
        走到头就可以找到解码字符，再将 node 重置为根节点
     */
    char[] chars = str.toCharArray();
    int i = 0;
    StringBuilder sb = new StringBuilder();
    Node node = root;

    while (i < chars.length) {
        if (!node.isLeaf()) { // 非叶子
            if(chars[i] == '0') { // 向左走
                node = node.left;
            } else if(chars[i] == '1') { // 向右走
                node = node.right;
            }
            i++;
        }
        if (node.isLeaf()) {
            sb.append(node.ch);
            node = root;
        }
    }
    return sb.toString();
}

运行

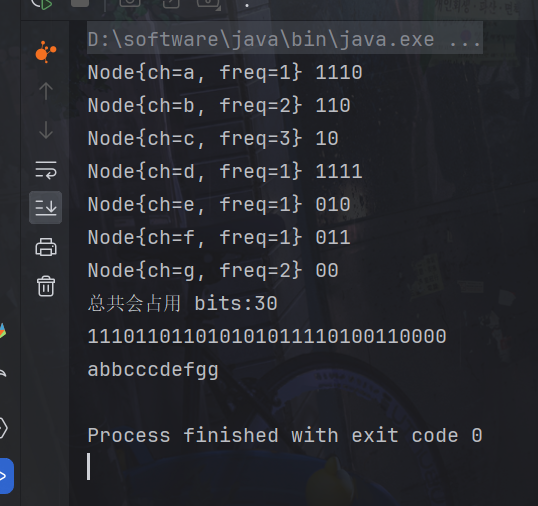
public static void main(String[] args) {
    HuffmanTree tree = new HuffmanTree("abbcccdefgg");
    String encoded = tree.encode();
    System.out.println(encoded);
    System.out.println(tree.decode(encoded));
}

参考

黑马数据结构