1.基本概述
动态规划是一种解决问题的算法思想,通常用于解决具有重叠子问题和最优子结构性质的问题。在动态规划中,通过将原问题分解为若干个子问题,先求解子问题的解,然后利用子问题的解来求解原问题的解。
动态规划通常的步骤:
- 定义状态:明确问题的状态,找出状态变量及其含义,例如数组、矩阵等。
- 确定状态转移方程:找出问题的状态之间的递推关系,即如何由小的子问题推导出大问题的解。
- 初始化边界条件:确定边界条件,即最小子问题的解,为递推过程提供基础。
- 计算顺序:根据状态转移方程,按照一定的顺序计算子问题的解,通常是自底向上或自顶向下。
2.求斐波那契第n项
回顾使用递归求解斐波那契第n项
public static int fibonacci(int n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
int x = fibonacci(n - 1);
int y = fibonacci(n - 2);
return x + y;
}使用动态优化
public static int fibonacci(int n) {
int[] dp = new int[n + 1]; // 用来缓存结果
dp[0] = 0;
dp[1] = 1;
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
for (int i = 2; i <= n ; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}动态规划一般可以用一维或二维数组来保存之前的计算结果,在这题可以进一步优化,使用变量存储。
public static int fibonacci2(int n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
int a = 0;
int b = 1;
for (int i = 2; i <= n ; i++) {
int c = b + a;
a = b;
b = c;
}
return b;
}
3.贝尔曼-福特算法求最短路径
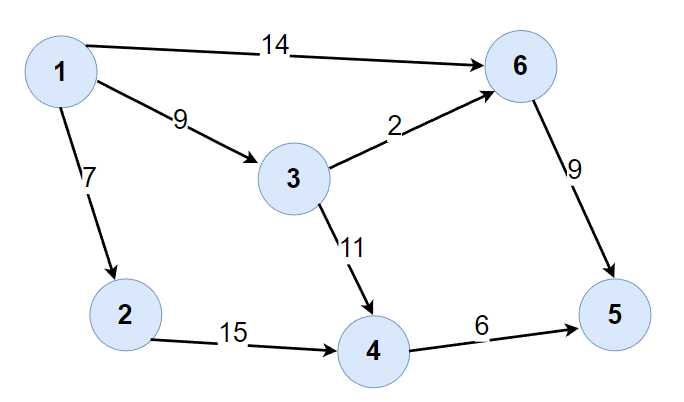
f(v) 用来表示从起点出发,到达 v 这个顶点的最短距离
公式:f(to) = min(f(to), f(from) + from.weight)
索引从1开始,大致流程:
v1 v2 v3 v4 v5 v6 0 ∞ ∞ ∞ ∞ ∞ 0 7 9 ∞ ∞ 14 第一轮 0 7 9 20 23 11 第二轮 0 7 9 20 20 11 第三轮 0 7 9 20 20 11 第四轮 0 7 9 20 20 11 第五轮
代码:
package com.dreams.dynamicprogramming;
import java.util.Arrays;
import java.util.List;
/**
* 贝尔曼-福特算法求最短路径
*/
public class BellmanFord {
static class Edge {
int from;
int to;
int weight;
public Edge(int from, int to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
}
public static void main(String[] args) {
List<Edge> edges = Arrays.asList(
new Edge(6, 5, 9),
new Edge(4, 5, 6),
new Edge(1, 6, 14),
new Edge(3, 6, 2),
new Edge(3, 4, 11),
new Edge(2, 4, 15),
new Edge(1, 3, 9),
new Edge(1, 2, 7)
);
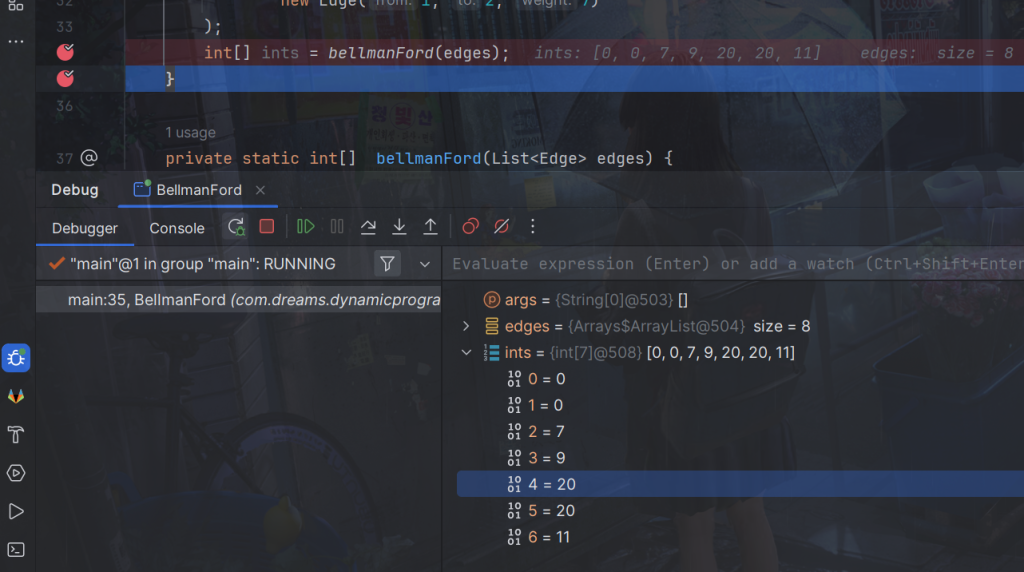
int[] ints = bellmanFord(edges);
}
private static int[] bellmanFord(List<Edge> edges) {
int[] dp = new int[7]; // 一维数组用来缓存结果
dp[1] = 0;
for (int i = 2; i < dp.length; i++) {
dp[i] = Integer.MAX_VALUE;
}
//循环顶点数量减1,因为这里索引从1开始,所以数组长度减2
for (int i = 0; i < dp.length - 2; i++) {
for (Edge e : edges) {
if (dp[e.from] != Integer.MAX_VALUE) {
dp[e.to] = Integer.min(dp[e.to], dp[e.from] + e.weight);
}
}
}
return dp;
}
}
4.不同路径


dp[i][j]表示从起始点到达网格中第i行第j列的位置的不同路径数。根据题目要求,机器人只能向下或向右移动,因此到达每个位置的路径数等于其上方格子的路径数加上其左侧格子的路径数。即:dp[i][j] = dp[i-1][j] + dp[i][j-1],边界条件是,当i=0或j=0时,机器人只能沿着边缘移动,因此在边缘上的位置的路径数都是1。
代码:
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n; j++) {
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}优化还可以使用一维数组
public int uniquePaths(int m, int n) {
int[] dp = new int[n];
for (int j = 0; j < n; j++) {
dp[j] = 1;
}
for (int i = 1; i < m; i++) {
dp[0] = 1;
for (int j = 1; j < n; j++) {
dp[j] = dp[j] + dp[j - 1];
}
}
return dp[n - 1];
}
5.0-1背包问题
1. n个物品都是固体,有重量和价值
2. 现在你要取走不超过 10克 的物品
3. 每次可以不拿或全拿,问最高价值是多少
编号 重量(g) 价值(元) 简称
1 4 1600 黄金一块 400 A
2 8 2400 红宝石一粒 300 R
3 5 30 白银一块 S
4 1 1_000_000 钻石一粒 D
演示:
0 1 2 3 4 5 6 7 8 9 10 0 0 0 0 0 A A A A A A A 黄金 1 0 0 0 0 A A A A R R R 红宝石 2 0 0 0 0 A A A A R R R 白银 3 0 D D D D DA DA DA DA DR DR 钻石
如果装不下,继承上一个状态的值,装得下,就选择最大价值。
if(装不下) {
dp[i][j] = dp[i-1][j]
} else { 装得下
dp[i][j] = max(dp[i-1][j], item.value + dp[i-1][j-item.weight])
}这个状态转移方程是动态规划解决0-1背包问题的核心:
- dp[i][j] 表示考虑前 i 个物品,背包容量为 j 时所能获得的最大价值。
- dp[i-1][j] 表示不选择当前物品 item 时的最大价值,即前 i-1 个物品放入容量为 j 的背包中所能获得的最大价值。
- item.value 表示当前物品的价值。
- dp[i-1][j-item.weight] 表示选择当前物品 item 并放入背包后,剩余空间为 j-item.weight 时所能获得的最大价值。
逻辑就是:
- 如果当前物品 item 的重量大于当前背包容量 j,则无法选择该物品,因此 dp[i][j] 等于不选择该物品时的最大价值,即 dp[i-1][j]。
- 如果当前物品 item 的重量小于等于当前背包容量 j,则可以选择放入或不放入该物品。若选择放入,则 dp[i][j] 等于选择当前物品时的最大价值,即 item.value + dp[i-1][j-item.weight];若选择不放入,则 dp[i][j] 等于不选择当前物品时的最大价值,即 dp[i-1][j]。取两者中的较大值作为 dp[i][j] 的值。
代码:
package com.dreams.dynamicprogramming;
import java.util.Arrays;
import java.util.stream.IntStream;
/**
* 0-1 背包问题 - 动态规划
*/
public class KnapsackProblem {
static class Item {
int index;
String name;
int weight;
int value;
public Item(int index, String name, int weight, int value) {
this.index = index;
this.name = name;
this.weight = weight;
this.value = value;
}
@Override
public String toString() {
return "Item(" + name + ")";
}
}
public static void main(String[] args) {
Item[] items = new Item[]{
new Item(1, "黄金", 4, 1600),
new Item(2, "宝石", 8, 2400),
new Item(3, "白银", 5, 30),
new Item(4, "钻石", 1, 10_000),
};
System.out.println(select(items, 10));
}
static int select(Item[] items, int total) {
int[][] dp = new int[items.length][total + 1];
Item item0 = items[0];
//赋值第一行
for (int j = 0; j < total + 1; j++) {
// 装得下
if (j >= item0.weight) {
dp[0][j] = item0.value;
} else {
// 装不下
dp[0][j] = 0;
}
}
for (int i = 1; i < dp.length; i++) {
Item item = items[i];
for (int j = 0; j < total + 1; j++) {
int x = dp[i - 1][j];
if (j >= item.weight) {
dp[i][j] = Integer.max(x,
// 上次剩余空间能装的最大价值 + 当前物品价值
dp[i - 1][j - item.weight] + item.value);
} else {
dp[i][j] = x;
}
}
}
return dp[dp.length - 1][total];
}
}
优化为一维数组,注意要从右边往回走,因为dp[j – item.weight])需要前面的数据
static int select(Item[] items, int total) {
int[] dp = new int[total + 1];
for (Item item : items) {
for (int j = total; j > 0; j--) {
if (j >= item.weight) { // 装得下
dp[j] = Integer.max(dp[j], item.value + dp[j - item.weight]);
}
}
System.out.println(Arrays.toString(dp));
}
return dp[total];
}
6.完全背包问题
过程:
0 1 2 3 4 5 6 1 0 0 c c cc cc ccc 青铜 重2 2 0 0 c s cc sc ccc 白银 重3 3 0 0 c s a a ac 黄金 重4
逻辑:
if(放得下) {
dp[i][j] = max(dp[i-1][j], dp[i][j-item.weight] + item.value)
} else {
dp[i][j] = dp[i-1][j]
}代码:
package com.dreams.dynamicprogramming;
import java.util.Arrays;
/**
* 完全背包问题 - 动态规划
*/
public class KnapsackProblemComplete {
static class Item {
int index;
String name;
int weight;
int value;
public Item(int index, String name, int weight, int value) {
this.index = index;
this.name = name;
this.weight = weight;
this.value = value;
}
@Override
public String toString() {
return "Item(" + name + ")";
}
}
public static void main(String[] args) {
Item[] items = new Item[]{
new Item(1, "青铜", 2, 3), // c
new Item(2, "白银", 3, 4), // s
new Item(3, "黄金", 4, 7), // a
};
System.out.println(select(items, 6));
}
private static int select(Item[] items, int total) {
int[][] dp = new int[items.length][total + 1];
Item item0 = items[0];
for (int j = 0; j < total + 1; j++) {
if (j >= item0.weight) {
dp[0][j] = dp[0][j - item0.weight] + item0.value;
}
}
for (int i = 1; i < items.length; i++) {
for (int j = 0; j < total + 1; j++) {
Item item = items[i];
int x = dp[i - 1][j]; // 上次的最大价值
if (j >= item.weight) {
//
dp[i][j] = Integer.max(x,
// 剩余空间能装的最大价值 + 当前物品价值
dp[i][j - item.weight] + item.value);
} else {
dp[i][j] = x;
}
}
}
return dp[items.length - 1][total];
}
}
注意:
dp[i][j] = Integer.max(x, dp[i][j – item.weight] + item.value);
这里不同0-1背包问题,这里是在当前行寻找,因为完全背包允许放置不限数量同样物品。
优化为一维数组
private static int select(Item[] items, int total) {
int[] dp = new int[total + 1];
for (Item item : items) {
for (int j = 0; j < total + 1; j++) {
if (j >= item.weight) {
dp[j] = Integer.max(dp[j], dp[j - item.weight] + item.value);
}
}
System.out.println(Arrays.toString(dp));
}
return dp[total];
}
7.零钱兑换

演示:
面值 0 1 2 3 4 5 1 0 1 11 111 1111 11111 2 0 1 2 21 22 221 5 0 1 2 21 22 5 总金额 - 类比为背包容量 硬币面值 - 类比为物品重量 硬币个数 - 类比为物品价值,固定为1 (求价值(个数)最小的)
逻辑:
if(装得下) {
// min(上次价值(个数), 剩余容量能装下的最小价值(个数)+1)
dp[i][j] = min(dp[i-1][j], dp[i][j-item.weight] + 1)
} else {
// 保留上次价值(个数)不变
dp[i][j] = dp[i-1][j]
}代码:
package com.dreams.dynamicprogramming;
import java.util.Arrays;
/**
* 零钱兑换 - 动态规划
* 凑成总金额的凑法中,需要硬币最少个数是几?
*/
public class ChangeMakingProblemLeetcode322 {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
// 0 max max max max max
Arrays.fill(dp, amount + 1);
dp[0] = 0;
System.out.println(Arrays.toString(dp));
for (int coin : coins) {
for (int j = coin; j < amount + 1; j++) {
dp[j] = Math.min(dp[j], 1 + dp[j - coin]);
}
System.out.println(Arrays.toString(dp));
}
int r = dp[amount];
//如果已经大于最大值,就是找不到,返回-1
return r > amount ? -1 : r;
}
public static void main(String[] args) {
ChangeMakingProblemLeetcode322 leetcode = new ChangeMakingProblemLeetcode322();
int count = leetcode.coinChange(new int[]{1, 2, 5}, 5);
System.out.println(count);
}
}
8.零钱兑换II


使用贪心算法可能出现错误答案,这里使用动态规划。
演示:
面值 0 1 2 3 4 5 总金额-背包容量
1 1 1 11 111 1111 11111
2 1 1 11 111 1111 11111
2 21 211 2111
22 221
5 1 1 11 111 1111 11111
2 21 211 2111
22 221
5逻辑:
if(放得下) dp[i][j] = dp[i-1][j] + dp[i][j-coin] else(放不下) dp[i][j] = dp[i-1][j]
代码:
package com.dreams.dynamicprogramming;
import java.util.Arrays;
import java.util.stream.IntStream;
/**
* 零钱兑换 II - 动态规划
* 凑成总金额有几种凑法?
*/
public class ChangeMakingProblemLeetcode518 {
public int change(int[] coins, int amount) {
int[][] dp = new int[coins.length][amount + 1];
for (int i = 0; i < coins.length; i++) {
dp[i][0] = 1;
}
for (int j = 1; j < amount + 1; j++) {
if (j >= coins[0]) {
dp[0][j] = dp[0][j - coins[0]];
}
}
for (int i = 1; i < coins.length; i++) {
for (int j = 1; j < amount + 1; j++) {
if (j >= coins[i]) {
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[coins.length - 1][amount];
}
public static void main(String[] args) {
ChangeMakingProblemLeetcode518 leetcode = new ChangeMakingProblemLeetcode518();
int count = leetcode.change(new int[]{25, 10, 5, 1}, 41);
System.out.println(count);
}
}一维数组优化:
package com.dreams;
public class Leetcode518 {
public int change(int amount, int[] coins) {
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] += dp[i - coin];
}
}
return dp[amount];
}
public static void main(String[] args) {
Leetcode518 leetcode = new Leetcode518();
int count = leetcode.change(5, new int[]{1, 2, 5});
System.out.println(count);
}
}
9.钢条切割问题
钢条各长度价值:
0 1 2 3 4 5 6 7 8 9 10 0 1 5 8 9 10 17 17 20 24 30
逻辑:
if(放得下)
dp[i][j]=max(dp[i-1][j],当前物品价值+dp[i][j-物品重量]
else(放不下)
dp[i][j]=dp[i-1][j]代码:
package com.dreams.dynamicprogramming;
/**
* 钢条切割问题 - 动态规划
*/
public class CutRodProblem {
static int cut(int[] values, int n) {
int[][] dp = new int[values.length][n + 1];
for (int i = 1; i < values.length; i++) {
for (int j = 1; j < n + 1; j++) {
if (j >= i) { // 放得下
dp[i][j] = Integer.max(dp[i - 1][j], values[i] + dp[i][j - i]);
} else { // 放不下
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[values.length - 1][n];
}
public static void main(String[] args) {
// 不同长度钢条的价值数组,数组的索引对应钢条的长度(物品重量)
System.out.println(cut(new int[]{0, 1, 5, 8, 9,}, 4)); // 10, 17, 17, 20, 24, 30
}
}
10.最长公共子串
演示:
d r e a m s r 0 1 0 0 0 0 e 0 0 2 0 0 0 a 0 0 0 3 0 0 s 0 0 0 0 0 1
逻辑:
if(相同字符) {
dp[i][j] = dp[i-1][j-1] + 1
} else {
dp[i][j] = 0
}代码:
package com.dreams.dynamicprogramming;
/**
* 最长公共子串
*/
public class LCSubstring {
static int lcs(String a, String b) {
int[][] dp = new int[b.length()][a.length()];
int max = 0;
for (int i = 0; i < b.length(); i++) {
for (int j = 0; j < a.length(); j++) {
if (a.charAt(j) == b.charAt(i)) {
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
max = Integer.max(max, dp[i][j]);
} else {
dp[i][j] = 0;
}
}
}
return max;
}
public static void main(String[] args) {
System.out.println(lcs("dreams", "reas"));
}
}
11.最长公共子序列

演示:
d r e a m d
0 0 0 0 0 0 0
r 0 0 1 1 1 1 1
e 0 0 1 2 2 2 2
a 0 0 1 2 3 3 3
s 0 0 1 2 2 2 3演示:
a b c d e
0 0 0 0 0 0
a 0 1 1 1 1 1
e 0 1 1 1 1 2
c 0 1 1 2 2 2演示:
a b c x y z 0 0 0 0 0 0 0 a 0 1 1 1 1 1 1 b 0 1 2 2 2 2 2 x 0 1 2 2 3 3 3 y 0 1 2 2 3 4 4 z 0 1 2 2 3 4 5
逻辑:
相同字符
找到上一行上一列数值+1
不同字符
max(上一行, 上一列)代码:
package com.dreams.dynamicprogramming;
/**
* 最长公共子序列
*/
public class LCSubsequence {
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length();
int n = text2.length();
char[] chars1 = text1.toCharArray();
char[] chars2 = text2.toCharArray();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i < m + 1; i++) {
char x = chars1[i - 1];
for (int j = 1; j < n + 1; j++) {
if (x == chars2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Integer.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
public static void main(String[] args) {
LCSubsequence code = new LCSubsequence();
System.out.println(code.longestCommonSubsequence("abcde", "aec"));
}
}注意:使用text1.toCharArray()得到字符数组用索引获取会比text1.charAt(j)快很多
参考