1.基本概述
跳表(Skip List)是一种用于有序元素的数据结构,它允许快速的搜索、插入和删除操作,其平均时间复杂度为O(log n),其中 n 是元素的数量。
跳表的核心思想是通过添加多级索引来加速搜索。每个节点都具有多个指针,这些指针跳过一定数量的节点,从而实现了快速的查找。最底层的指针指向链表中的下一个节点,而更高级的指针则可能跳过若干个节点。
跳表的高效性取决于索引层的构建,通常情况下,跳表会以一定的概率构建多级索引,这样可以在保证效率的同时节省空间。跳表的平均时间复杂度与二叉搜索树相似,但它的实现相对简单,并且可以在不需要严格平衡的情况下维护平衡性。
跳表的设计使其成为一种在并发环境下更容易实现的数据结构,因为跳表的插入和删除操作不需要像平衡树那样频繁地进行旋转操作来保持平衡。它在很多应用中被广泛使用,例如在Redis等内存数据库中,用于实现有序集合。
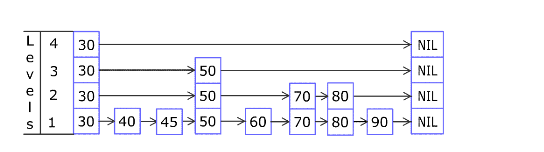
跳表查找的逻辑:
- 采用类似下楼梯方式查找。
- 若 next 指针为 null,或者 next 指向的节点值>=目标,向下找。
- 若 next 指针不为 null,且 next 指向的节点值 < 目标,向右找。
2.代码演示
例如leetcode这题


代码:
package com.dreams.leetcode;
import java.util.Arrays;
import java.util.Random;
/**
* 跳表
*/
public class Leetcode1206 {
public static void main(String[] args) {
Skiplist list = new Skiplist();
Skiplist.Node head = list.head;
Skiplist.Node n3 = new Skiplist.Node(3);
Skiplist.Node n7 = new Skiplist.Node(7);
Skiplist.Node n11 = new Skiplist.Node(11);
Skiplist.Node n12 = new Skiplist.Node(12);
Skiplist.Node n16 = new Skiplist.Node(16);
Skiplist.Node n19 = new Skiplist.Node(19);
Skiplist.Node n22 = new Skiplist.Node(22);
Skiplist.Node n23 = new Skiplist.Node(23);
Skiplist.Node n26 = new Skiplist.Node(26);
Skiplist.Node n30 = new Skiplist.Node(30);
Skiplist.Node n37 = new Skiplist.Node(37);
head.next[0] = head.next[1] = head.next[2] = n3;
head.next[3] = head.next[4] = head.next[5] = head.next[6] = head.next[7] = n19;
n3.next[0] = n3.next[1] = n3.next[2] = n7;
n7.next[0] = n11;
n7.next[1] = n12;
n7.next[2] = n16;
n11.next[0] = n12;
n12.next[0] = n12.next[1] = n16;
n16.next[0] = n16.next[1] = n16.next[2] = n19;
n19.next[0] = n19.next[1] = n19.next[2] = n22;
n19.next[3] = n26;
n22.next[0] = n23;
n22.next[1] = n22.next[2] = n26;
n23.next[0] = n26;
n26.next[0] = n30;
n26.next[1] = n37;
n30.next[0] = n37;
System.out.println(Arrays.toString(list.find(30)));
}
static Random r = new Random();
static int randomLevel(int max) {
int x = 1;
while (x < max) {
if (r.nextBoolean()) {
return x;
}
x++;
}
return x;
}
static class Skiplist {
private static final int MAX = 10; // redis 32 java 62
private final Node head = new Node(-1);
static class Node {
int val; // 值
Node[] next = new Node[MAX]; // next 数组
public Node(int val) {
this.val = val;
}
@Override
public String toString() {
return "Node(" + val + ")";
}
}
public Node[] find(int val) {
Node[] path = new Node[MAX];
Node curr = head;
for (int level = MAX - 1; level >= 0; level--) { // 从上向下找
while (curr.next[level] != null && curr.next[level].val < val) { // 向右找
curr = curr.next[level];
}
path[level] = curr;
}
return path;
}
public boolean search(int val) {
Node[] path = find(val);
Node node = path[0].next[0];
return node != null && node.val == val;
}
public void add(int val) {
// 1. 确定添加位置(把 val 当作目标查询,经历的路径就可以确定添加位置)
Node[] path = find(val);
// 2. 创建新节点随机高度
Node node = new Node(val);
int level = randomLevel(MAX);
// 3. 修改路径节点 next 指针,以及新节点 next 指针
for (int i = 0; i < level; i++) {
node.next[i] = path[i].next[i];
path[i].next[i] = node;
}
}
public boolean erase(int val) {
Node[] path = find(val);
Node node = path[0].next[0];
if (node == null || node.val != val) {
return false;
}
for (int i = 0; i < MAX; i++) {
if (path[i].next[i] != node) {
break;
}
path[i].next[i] = node.next[i];
}
return true;
}
}
}
参考