什么是快速幂?
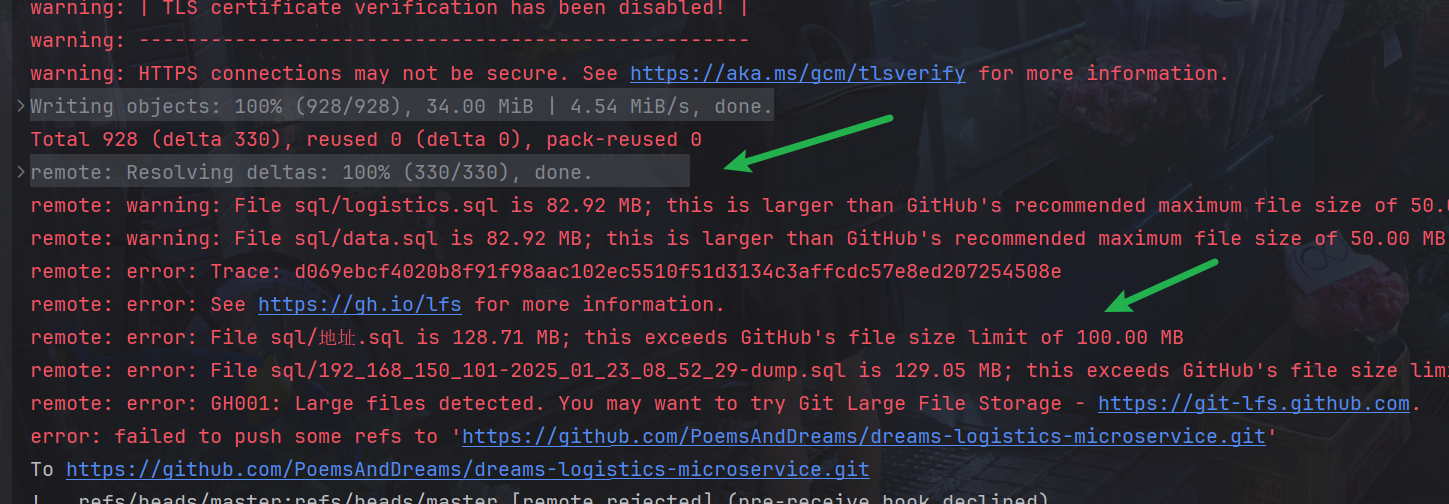
比如求解
12的二进制是1100
那么可以看成
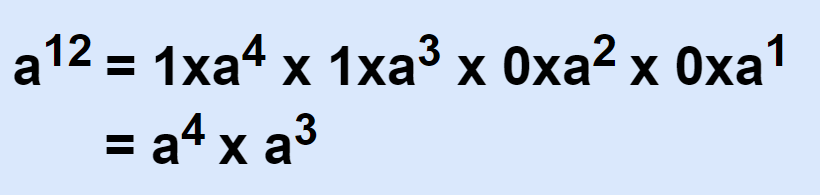
而什么是矩阵快速幂呢?
如图一个斐波那契数列
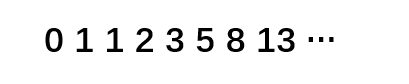
我们假设以两位数为一个矩阵
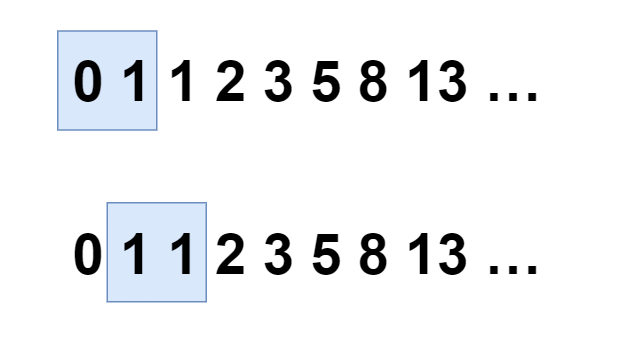
设该矩阵
假设乘一个未知矩阵,可得下一个矩阵,
如图:
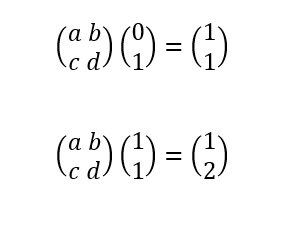
易解的a,b,c,d的值,如图:
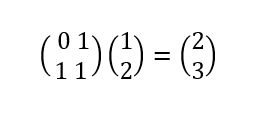
易得如图规律
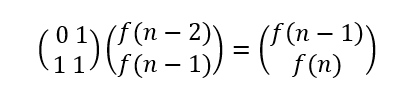
注意:
这里的n表示斐波那契数列的第三位,也就是从第三位开始求起来
那么求n的值就等于与原始矩阵相乘n位
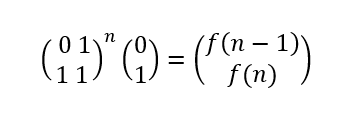
那么就转变为快速幂求法,这就是矩阵快速幂
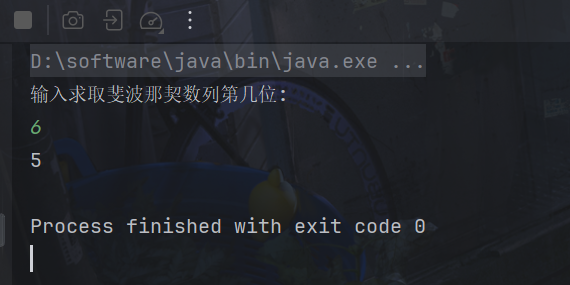
代码如下:
package com.dreams;
/**
* @author PoemsAndDreams
* @date 2023-11-05 20:54
*/
public class Sunday_11_5 {
public static void main(String[] args) {
System.out.println("输入求取斐波那契数列第几位");
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
if (n == 1) {
System.out.println(0);
return;
}
if (n == 2) {
System.out.println(1);
return;
}
//注意n值从第三位求起,所以对其应先减二
n = n - 2;
int[] result = reResult(n);
System.out.println(result[1]);
}
public static int[] reResult(int n) {
int[][] ints = {{0, 1}, {1, 1}};
int[] fn = {0, 1};
while (n > 0) {
if ((n & 1) == 1) {
fn = count(ints, fn);
}
n >>= 1;
ints = countATA(ints, ints);
}
return fn;
}
public static int[] count(int[][] left, int[] right) {
int[] result = new int[left.length];
for (int i = 0; i < left.length; i++) {
for (int j = 0; j < left.length; j++) {
result[i] = result[i] + left[i][j] * right[j];
}
}
return result;
}
private static int[][] countATA(int[][] AT, int[][] A) {
int[][] ATA = new int[AT.length][A[0].length];
for (int i = 0; i < ATA.length; i++) {
for (int j = 0; j < ATA[0].length; j++) {
for (int k = 0; k < AT[0].length; k++) {
ATA[i][j] = ATA[i][j] + AT[i][k] * A[k][j];
}
}
}
return ATA;
}
}
注意:
过大的数可能超过了int的存储范围,所以不再正确,可以换成其他存储。