来自leetcode295

一个解决思路是
使用了两个堆来实现。左边的堆为大顶堆,右边的堆为小顶堆。添加元素时,根据两边堆的大小,将新元素加入到对应的堆中,并且保持左右两边的数据量平衡。如果两边数据量一样,则将新元素加入右边,并将右边堆的最小值弹出并加入到左边堆中;如果右边数据量多,则将新元素加入左边,并将左边堆的最大值弹出并加入到右边堆中。
查找中位数时,如果左右两边的数据量一样,则取左右堆顶元素的平均值作为中位数;如果左边数据量多,则直接取左边堆顶元素作为中位数。
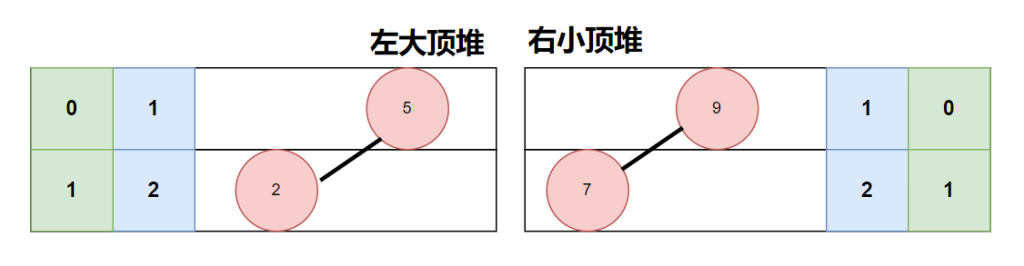
左边的堆为大顶堆,右边的堆为小顶堆
可以使用java的堆实现
// 大顶堆
private PriorityQueue<Integer> left = new PriorityQueue<>(
(a, b) -> Integer.compare(b, a) //
);
// 小顶堆
private PriorityQueue<Integer> right = new PriorityQueue<>(
(a, b) -> Integer.compare(a, b) //
);
下面就是解决思路重要逻辑
添加函数。
public void addNum(int num) {
//保证两边数据量的平衡,规定两边个数一样时,左边个数加一
if (left.size() == right.size()) {
//左边个数加一时, 把新元素加在右边,弹出右边最小的加入左边
right.offer(num);
left.offer(right.poll());
} else {
//右边个数加一时, 把新元素加在左边,弹出左边最小的加入右边
left.offer(num);
right.offer(left.poll());
}
}两边数据一致, 左右各取堆顶元素求平均
public double findMedian() {
if (left.size() == right.size()) {
return (left.peek() + right.peek()) / 2.0;
} else {
//左边多一个, 取左边堆顶元素
return left.peek();
}
}