leetcode104题
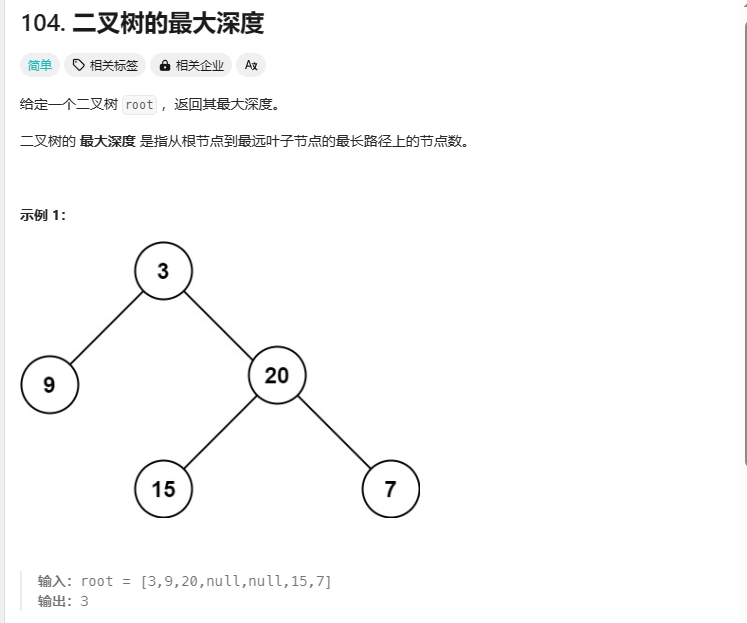

递归解决,在这题里,该方法效率最高
public int maxDepth(TreeNode node) {
if (node == null) {
return 0;
}
int d1 = maxDepth(node.left);
int d2 = maxDepth(node.right);
return Integer.max(d1, d2) + 1;
}
使用非递归后序遍历解决
首先定义了一个变量 max 来记录栈的最大高度,初始化为 0。使用一个 while 循环来遍历二叉树节点,循环条件为当前节点不为空或者栈不为空。在循环中,首先判断当前节点是否为空,如果不为空,则将当前节点入栈,并更新栈的大小,然后比较当前栈的大小与 max 的值,更新 max 为更大的那个。如果当前节点为空,则说明到达了某个叶子节点,此时需要判断栈顶节点的右子树是否已经遍历过,如果已经遍历过或者为空,则将栈顶节点出栈;否则,将当前节点移动到栈顶节点的右子树。最终返回 max 值,即栈的最大高度,也即二叉树的最大深度。
public int maxDepth(TreeNode root) {
TreeNode curr = root;
TreeNode pop = null;
LinkedList<TreeNode> stack = new LinkedList<>();
int max = 0; // 栈的最大高度
while (curr != null || !stack.isEmpty()) {
if (curr != null) {
stack.push(curr);
int size = stack.size();
if (size > max) {
max = size;
}
curr = curr.left;
} else {
TreeNode peek = stack.peek();
if (peek.right == null || peek.right == pop) {
pop = stack.pop();
} else {
curr = peek.right;
}
}
}
return max;
}
使用层序遍历, 层数即最大深度
首先判断根节点是否为空,如果为空则直接返回深度为 0。创建一个队列 queue,并将根节点加入队列。使用一个 while 循环遍历队列,直到队列为空为止。在每一层遍历中,获取当前队列的大小,表示当前层的节点个数。遍历当前层的所有节点,依次弹出队列中的节点,如果节点有左子树,则将左子树节点加入队列;如果节点有右子树,则将右子树节点加入队列。每完成一层的遍历,深度加一。最终返回计算得到的深度值。
当前层for循环次数为上一层添加左右子节点后队列的数量,那么刚好循环完该层。
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int depth = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode poll = queue.poll();
if (poll.left != null) {
queue.offer(poll.left);
}
if (poll.right != null) {
queue.offer(poll.right);
}
}
depth ++;
}
return depth;
}
参考