1.冒泡排序
冒泡排序在比较相邻元素时,只有在它们的大小关系不符合排序顺序时才会进行交换,而对于相等的元素,它们之间的相对位置不会改变,所以冒泡排序是稳定的。
代码:
// 冒泡排序算法
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 交换元素位置
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}引入一个标志位来表示是否发生了交换。如果在一轮遍历中没有发生交换,就可以提前结束排序,因为数组已经是有序的了。这样可以减少不必要的比较,提高性能。
// 优化的冒泡排序算法
public static void bubbleSort(int[] arr) {
int n = arr.length;
boolean swapped;
for (int i = 0; i < n - 1; i++) {
swapped = false;
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 交换元素位置
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true;
}
}
// 如果没有发生交换,说明数组已经有序,提前退出循环
if (!swapped) {
break;
}
}
}
2.选择排序
选择排序(Selection Sort)是一种简单直观的排序算法,它的基本思想是每次从待排序的数据中选择最小(或最大)的元素,放到已排序序列的末尾(或开头),直到所有元素都被排序完毕。
它是不稳定的算法。
public static void selectionSort(int[] a) {
// 1. 选择轮数 a.length - 1
// 2. 交换的索引位置(right) 初始 a.length - 1, 每次递减
for (int right = a.length - 1; right > 0 ; right--) {
int max = right;
for (int i = 0; i < right; i++) {
if (a[i] > a[max]) {
max = i;
}
}
if(max != right) {
int t = a[max];
a[max] = a[right];
a[right] = t;
}
}
}
3.堆排序
堆排序(Heap Sort)是一种基于堆数据结构的排序算法,它利用了堆的性质来进行排序。堆排序的基本思想是先将待排序的元素构建成一个最大堆(或最小堆),然后依次将堆顶元素(最大元素或最小元素)与堆的最后一个元素交换,并重新调整堆,使得剩余元素重新构成一个堆,然后重复这个过程,直到所有元素都被排序完毕。
它是不稳定的算法
package com.dreams.sort;
import java.util.Arrays;
/**
* 堆排序
*/
public class HeapSort {
public static void sort(int[] a) {
heapify(a, a.length);
for (int right = a.length - 1; right > 0; right--) {
swap(a, 0, right);
down(a, 0, right);
}
}
// 建堆 O(n)
private static void heapify(int[] array, int size) {
for (int i = size / 2 - 1; i >= 0; i--) {
down(array, i, size);
}
}
// 下潜
// leetcode 上数组排序题目用堆排序求解,非递归实现比递归实现大约快 6ms
private static void down(int[] array, int parent, int size) {
while (true) {
int left = parent * 2 + 1;
int right = left + 1;
int max = parent;
if (left < size && array[left] > array[max]) {
max = left;
}
if (right < size && array[right] > array[max]) {
max = right;
}
if (max == parent) { // 没找到更大的孩子
break;
}
swap(array, max, parent);
parent = max;
}
}
// 交换
private static void swap(int[] a, int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
int[] a = {2, 3, 1, 7, 6, 4, 5};
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
}
4.插入排序
插入排序是一种简单直观的排序算法,它的工作原理是通过构建有序序列,对未排序的数据逐个进行插入,从而达到排序的目的。
代码:
package com.dreams.sort;
import java.util.Arrays;
/**
* 插入排序
*/
public class InsertionSort {
public static void sort(int[] a) {
for (int low = 1; low < a.length; low++) {
int t = a[low];
int i = low - 1;
// 自右向左找插入位置,如果比待插入元素大,则不断右移,空出插入位置
while (i >= 0 && t < a[i]) {
a[i + 1] = a[i];
i--;
}
// 找到插入位置
if (i != low - 1) {
a[i + 1] = t;
}
}
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 5, 8, 1, 4};
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
}
5.希尔排序
希尔排序(Shell Sort)是一种改进的插入排序算法,也称为缩小增量排序。希尔排序的基本思想是将原始序列分割成若干个子序列,对这些子序列分别进行插入排序,然后逐步缩小子序列的间隔,最终完成排序。
package com.dreams.sort;
import java.util.Arrays;
/**
* 希尔排序
*/
public class ShellSort {
public static void sort(int[] a) {
for (int gap = a.length >> 1; gap >= 1; gap = gap >> 1) {
// gap=4
for (int low = gap; low < a.length; low++) {
int t = a[low]; // t=5
int i = low - gap;
// 自右向左找插入位置,如果比待插入元素大,则不断右移,空出插入位置
while (i >= 0 && t < a[i]) {
a[i + gap] = a[i];
i -= gap;
}
// 找到插入位置
if (i != low - gap) {
a[i + gap] = t;
}
}
}
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 5, 8, 1, 4};
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
}
6.归并排序
归并排序(Merge Sort)是一种基于分治思想的排序算法,它将待排序的序列递归地分成两个子序列,直到每个子序列只有一个元素为止,然后将相邻的子序列两两合并,同时将合并后的子序列排序,最终得到完全有序的序列。
稳定算法
自顶至下
代码:
package com.dreams.sort;
import java.util.Arrays;
/**
* 归并排序 TopDown
*/
public class MergeSortTopDown {
/*
a1 原始数组
i~iEnd 第一个有序范围
j~jEnd 第二个有序范围
a2 临时数组
*/
public static void merge(int[] a1, int i, int iEnd, int j, int jEnd, int[] a2) {
int k = i;
while (i <= iEnd && j <= jEnd) {
if (a1[i] < a1[j]) {
a2[k] = a1[i];
i++;
} else {
a2[k] = a1[j];
j++;
}
k++;
}
if (i > iEnd) {
System.arraycopy(a1, j, a2, k, jEnd - j + 1);
}
if (j > jEnd) {
System.arraycopy(a1, i, a2, k, iEnd - i + 1);
}
}
public static void sort(int[] a1) {
int[] a2 = new int[a1.length];
split(a1, 0, a1.length - 1, a2);
}
private static void split(int[] a1, int left, int right, int[] a2) {
// 2. 治
if (left == right) {
return;
}
// 1. 分
int m = (left + right) >>> 1;
split(a1, left, m, a2); // left = 0 m = 0 9
split(a1, m + 1, right, a2); // m+1 = 1 right = 1 3
// 3. 合
merge(a1, left, m, m + 1, right, a2);
System.arraycopy(a2, left, a1, left, right - left + 1);
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 8, 5, 1, 4};
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
}
自下至上
就是非递归
代码:
package com.dreams.sort;
import java.util.Arrays;
/**
* 归并排序 BottomUp
*/
public class MergeSortBottomUp {
/*
a1 原始数组
i~iEnd 第一个有序范围
j~jEnd 第二个有序范围
a2 临时数组
*/
public static void merge(int[] a1, int i, int iEnd, int j, int jEnd, int[] a2) {
int k = i;
while (i <= iEnd && j <= jEnd) {
if (a1[i] < a1[j]) {
a2[k] = a1[i];
i++;
} else {
a2[k] = a1[j];
j++;
}
k++;
}
if (i > iEnd) {
System.arraycopy(a1, j, a2, k, jEnd - j + 1);
}
if (j > jEnd) {
System.arraycopy(a1, i, a2, k, iEnd - i + 1);
}
}
public static void sort(int[] a1) {
int n = a1.length;
int[] a2 = new int[n];
// width 代表有序区间的宽度,取值依次为 1、2、4 ...
for (int width = 1; width < n; width *= 2) {
// [left, right] 分别代表待合并区间的左右边界
for (int left = 0; left < n; left += 2 * width) {
int right = Math.min(left + 2 * width - 1, n - 1);
// System.out.printf("width %d [%d,%d]%n", width, left, right);
int m = Math.min(left + width - 1, n - 1);
merge(a1, left, m, m + 1, right, a2);
}
System.arraycopy(a2, 0, a1, 0, n);
}
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 8, 5, 1, 4};
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
}
归并加入插入排序
package com.dreams.sort;
import java.util.Arrays;
/**
* 归并排序 + 插入排序
*/
public class MergeInsertionSort {
public static void insertion(int[] a, int left, int right) {
for (int low = left + 1; low <= right; low++) {
int t = a[low];
int i = low - 1;
// 自右向左找插入位置,如果比待插入元素大,则不断右移,空出插入位置
while (i >= left && t < a[i]) {
a[i + 1] = a[i];
i--;
}
// 找到插入位置
if (i != low - 1) {
a[i + 1] = t;
}
}
}
public static void merge(int[] a1, int i, int iEnd, int j, int jEnd, int[] a2) {
int k = i;
while (i <= iEnd && j <= jEnd) {
if (a1[i] < a1[j]) {
a2[k] = a1[i];
i++;
} else {
a2[k] = a1[j];
j++;
}
k++;
}
if (i > iEnd) {
System.arraycopy(a1, j, a2, k, jEnd - j + 1);
}
if (j > jEnd) {
System.arraycopy(a1, i, a2, k, iEnd - i + 1);
}
}
public static void sort(int[] a1) {
int[] a2 = new int[a1.length];
split(a1, 0, a1.length - 1, a2);
}
private static void split(int[] a1, int left, int right, int[] a2) {
// 2. 治
if (right - left <= 32) {
// 插入排序
insertion(a1, left, right);
return;
}
// 1. 分
int m = (left + right) >>> 1;
split(a1, left, m, a2);
split(a1, m + 1, right, a2);
// 3. 合
merge(a1, left, m, m + 1, right, a2);
System.arraycopy(a2, left, a1, left, right - left + 1);
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 8, 5, 1, 4};
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
}
7.快速排序
快速排序是一种常用的排序算法,其基本思想是通过将数组分割成较小的子数组,然后递归地排序这些子数组。
步骤如下:
- 选择一个基准元素(pivot),通常选择数组的第一个元素。
- 将数组中小于基准元素的元素移到基准元素的左边,大于基准元素的元素移到基准元素的右边,基准元素则处于最终排好序的位置。
- 对基准元素左右两边的子数组分别递归地执行步骤 1 和步骤 2,直到各个子数组的大小为 1 或 0,表示已经排好序。
单边循环(lomuto分区)
- 选择最右侧元素作为基准点
- j 找比基准点小的,i 找比基准点大的,一旦找到,二者进行交换
- 最后基准点与 i交换,i即为基准点最终索引
package com.dreams.sort;
import java.util.Arrays;
/**
* 单边循环快排(lomuto 洛穆托分区方案)
*/
public class QuickSortLomuto {
public static void sort(int[] a) {
quick(a, 0, a.length - 1);
}
private static void quick(int[] a, int left, int right) {
if (left >= right) {
return;
}
int p = partition(a, left, right); // p代表基准点元素索引
quick(a, left, p - 1);
quick(a, p + 1, right);
}
private static int partition(int[] a, int left, int right) {
int pv = a[right]; // 基准点元素值
int i = left;
int j = left;
while (j < right) {
if (a[j] < pv) { // j 找到比基准点小的了, 没找到大的
if (i != j) {
swap(a, i, j);
}
i++;
}
j++;
}
swap(a, i, right);
return i;
}
private static void swap(int[] a, int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
int[] a = {5, 3, 7, 2, 9, 8, 1, 4};
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
}
双边循环
- 选择最左侧元素作为基准点
- j找比基准点小的,i 找比基准点大的,一旦找到,二者进行交换,i从左向右。j从右向左
- 最后基准点与i交换,i即为基准点最终索引
代码:
要先处理 j,再处理 i,顺序不能变。
package com.dreams.sort;
import java.util.Arrays;
import java.util.concurrent.ThreadLocalRandom;
/**
* 双边循环快排
*/
public class QuickSortHoare {
public static void sort(int[] a) {
quick(a, 0, a.length - 1);
}
private static void quick(int[] a, int left, int right) {
if (left >= right) {
return;
}
int p = partition(a, left, right);
quick(a, left, p - 1);
quick(a, p + 1, right);
}
/*
注意事项
1. 为啥要加内层循环的 i<j 条件
2. 为啥要先处理 j,再处理 i
3. 随机元素作为基准点
4. 如果有大量重复元素
*/
private static int partition(int[] a, int left, int right) {
int idx = ThreadLocalRandom.current().nextInt(right - left + 1) + left;
// [0~9] right-left+1=3 [0,2]+4=[4,6]
swap(a, idx, left);
int pv = a[left];
int i = left;
int j = right;
while (i < j) {
// 1. j 从右向左找小(等)的
while (i < j && a[j] > pv) {
j--;
}
// 2. i 从左向右找大的
while (i < j && a[i] <= pv) {
i++;
}
// 3. 交换位置
swap(a, i, j);
}
swap(a, left, i);
return i;
}
private static void swap(int[] a, int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 8, 5, 1, 4};
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
}
处理相等元素
代码:
package com.dreams.sort;
import java.util.Arrays;
import java.util.concurrent.ThreadLocalRandom;
/**
* 双边循环快排 - 处理相等元素
*/
public class QuickSortHandleDuplicate {
public static void sort(int[] a) {
quick(a, 0, a.length - 1);
}
private static void quick(int[] a, int left, int right) {
if (left >= right) {
return;
}
int p = partition(a, left, right);
quick(a, left, p - 1);
quick(a, p + 1, right);
}
/*
循环内
i 从 left + 1 开始,从左向右找大的或相等的
j 从 right 开始,从右向左找小的或相等的
交换,i++ j--
循环外 j 和 基准点交换,j 即为分区位置
*/
private static int partition(int[] a, int left, int right) {
int idx = ThreadLocalRandom.current().nextInt(right - left + 1) + left;
swap(a, left, idx);
int pv = a[left];
int i = left + 1;
int j = right;
while (i <= j) {
// i 从左向右找大的或者相等的
while (i <= j && a[i] < pv) {
i++;
}
// j 从右向左找小的或者相等的
while (i <= j && a[j] > pv) {
j--;
}
if (i <= j) {
swap(a, i, j);
i++;
j--;
}
}
swap(a, j, left);
return j;
}
private static void swap(int[] a, int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
// int[] a = {4, 2, 1, 3, 2, 4}; // 最外层循环 = 要加
// int[] a = {2, 1, 3, 2}; // 内层循环 = 要加
int[] a = {2, 1, 3, 2}; // 内层if要加
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
}
8.计数排序
计数排序是一种非比较性的排序算法,适用于待排序元素范围较小的情况。它通过统计每个元素出现的次数,然后根据这些统计信息确定每个元素在排序后的位置。
基本步骤:
- 找到最大值,创建一个大小为 最大值+1 的 count 数组
- count 数组的索引对应原始数组的元素,用来统计该元素的出现次数
- 遍历 count 数组,根据 count 数组的索引(即原始数组的元素)以及出现次数,生成排序后内容,count 数组的索引是:已排序好的
- 前提:待排序元素 >=0 且最大值不能太大。
代码:
package com.dreams.sort;
import java.util.Arrays;
/**
* 计数排序(处理 >= 0 的元素)
*/
public class CountingSortPositive {
/*
要点
1. 找到最大值,创建一个大小为 最大值+1 的 count 数组
2. count 数组的索引对应原始数组的元素,用来统计该元素的出现次数
3. 遍历 count 数组,根据 count 数组的索引(即原始数组的元素)以及出现次数,生成排序后内容
count 数组的索引是:已排序好的
前提:待排序元素 >=0 且最大值不能太大
*/
public static void main(String[] args) {
int[] a = {5, 1, 1, 3, 0, -1}; // 5+1=6
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
/*
{5, 1, 1, 3, 0} 原始数组 a
[1 2 0 1 0 1] count
0 1 2 3 4 5
*/
public static void sort(int[] a) {
// 1. 准备 count 数组
int max = a[0];
for (int i = 1; i < a.length; i++) {
if (a[i] > max) {
max = a[i];
}
}
int[] count = new int[max + 1];
// 2. 用 count 数组记录各个元素出现次数,索引对应元素
for (int v : a) { // v 原始数组的元素
count[v]++;
}
// 3. 从 count 数组取出索引,即排好序的元素
int k = 0;
for (int i = 0; i < count.length; i++) {
// i 代表原始数组元素 count[i] 元素出现次数
while (count[i] > 0) {
a[k++] = i;
count[i]--;
}
}
}
}
改进:
package com.dreams.sort;
import java.util.Arrays;
/**
* 计数排序
*/
public class CountingSort {
/*
要点
1. 让原始数组的最小值映射到 count[0] 最大值映射到 count 最右侧
2. 原始数组元素 - 最小值 = count 索引
3. count 索引 + 最小值 = 原始数组元素
*/
public static void main(String[] args) {
int[] a = {5, 1, 1, 3, 0, -1};
System.out.println(Arrays.toString(a));
sort(a);
System.out.println(Arrays.toString(a));
}
// 2N + K n*log(n)
/*
{5, 1, 1, 3, 0, -1} 原始数组 a
[1 1 2 0 1 0 1 ] count
0 1 2 3 4 5 6
-1 0 1 3 5
*/
public static void sort(int[] a) {
int max = a[0];
int min = a[0];
for (int i = 1; i < a.length; i++) {
if (a[i] > max) {
max = a[i];
}
if (a[i] < min) {
min = a[i];
}
}
int[] count = new int[max - min + 1];
for (int v : a) { // v 原始数组元素 - 最小值 = count 索引
count[v - min]++;
}
//System.out.println(Arrays.toString(count));
int k = 0;
for (int i = 0; i < count.length; i++) {
// i + min 代表原始数组元素 count[i] 元素出现次数
while (count[i] > 0) {
a[k++] = i + min;
count[i]--;
}
}
}
}
9.桶排序
桶排序是一种排序算法,它将待排序的元素分散到若干个“桶”中,然后对每个桶中的元素进行排序,最后按照桶的顺序以及每个桶内元素的顺序将它们合并成有序序列。
我们需要一个动态数组
package com.dreams.datastructure.array;
import java.util.Arrays;
import java.util.Iterator;
import java.util.function.Consumer;
import java.util.stream.IntStream;
/**
* 动态数组
*/
public class DynamicArray implements Iterable<Integer> {
private int size = 0; // 逻辑大小
private int capacity = 8; // 容量
private int[] array = {};
public int[] array() {
return Arrays.copyOf(array, size);
}
/**
* 向最后位置 [size] 添加元素
*
* @param element 待添加元素
*/
public void addLast(int element) {
add(size, element);
}
/**
* 向 [0 .. size] 位置添加元素
*
* @param index 索引位置
* @param element 待添加元素
*/
public void add(int index, int element) {
checkAndGrow();
// 添加逻辑
if (index >= 0 && index < size) {
// 向后挪动, 空出待插入位置
System.arraycopy(array, index,
array, index + 1, size - index);
}
array[index] = element;
size++;
}
private void checkAndGrow() {
// 容量检查
if (size == 0) {
array = new int[capacity];
} else if (size == capacity) {
// 进行扩容, 1.5 1.618 2
capacity += capacity >> 1;
int[] newArray = new int[capacity];
System.arraycopy(array, 0,
newArray, 0, size);
array = newArray;
}
}
/**
* 从 [0 .. size) 范围删除元素
*
* @param index 索引位置
* @return 被删除元素
*/
public int remove(int index) { // [0..size)
int removed = array[index];
if (index < size - 1) {
// 向前挪动
System.arraycopy(array, index + 1,
array, index, size - index - 1);
}
size--;
return removed;
}
/**
* 查询元素
*
* @param index 索引位置, 在 [0..size) 区间内
* @return 该索引位置的元素
*/
public int get(int index) {
return array[index];
}
/**
* 遍历方法1
*
* @param consumer 遍历要执行的操作, 入参: 每个元素
*/
public void foreach(Consumer<Integer> consumer) {
for (int i = 0; i < size; i++) {
// 提供 array[i]
// 返回 void
consumer.accept(array[i]);
}
}
/**
* 遍历方法2 - 迭代器遍历
*/
@Override
public Iterator<Integer> iterator() {
return new Iterator<Integer>() {
int i = 0;
@Override
public boolean hasNext() { // 有没有下一个元素
return i < size;
}
@Override
public Integer next() { // 返回当前元素,并移动到下一个元素
return array[i++];
}
};
}
/**
* 遍历方法3 - stream 遍历
*
* @return stream 流
*/
public IntStream stream() {
return IntStream.of(Arrays.copyOfRange(array, 0, size));
}
}
桶排序代码:
桶内元素使用我们写过的插入排序即可。
package com.dreams.sort;
import com.dreams.datastructure.array.DynamicArray;
import java.util.Arrays;
/**
* 桶排序
*/
public class BucketSort {
public static void main(String[] args) {
int[] ages = {20, 18, 28, 66, 25, 31, 67, 30}; // 假设人类年龄 1~99
System.out.println(Arrays.toString(ages));
sort(ages);
System.out.println(Arrays.toString(ages));
}
/*
0
1 18
2 20 25 28
3 31
4
5
6 66 67
7
8
9
*/
public static void sort(int[] ages) {
// 1. 准备桶
DynamicArray[] buckets = new DynamicArray[10];
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new DynamicArray();
}
// 2. 放入年龄数据
for (int age : ages) {
buckets[age / 10].addLast(age);
}
int k = 0;
for (DynamicArray bucket : buckets) {
// 3. 排序桶内元素
int[] array = bucket.array();
InsertionSort.sort(array);
System.out.println(Arrays.toString(array));
// 4. 把每个桶排序好的内容,依次放入原始数组
for (int v : array) {
ages[k++] = v;
}
}
}
}
代码改进:
主要是桶数量的优化。
package com.dreams.sort;
import com.dreams.datastructure.array.DynamicArray;
import java.util.Arrays;
/**
* 桶排序(改进)
*/
public class BucketSortGeneric {
public static void main(String[] args) {
int[] ages = {9, 0, 5, 1, 3, 2, 4, 6, 8, 7};
System.out.println(Arrays.toString(ages));
int max = ages[0];
int min = ages[0];
for (int i = 1; i < ages.length; i++) {
if (ages[i] > max) {
max = ages[i];
}
if (ages[i] < min) {
min = ages[i];
}
}
// 1. 准备桶
DynamicArray[] buckets = new DynamicArray[(max - min) / 3 + 1];
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new DynamicArray();
}
// 2. 放入数据
for (int age : ages) {
buckets[(age - min) / 3].addLast(age);
}
int k = 0;
for (DynamicArray bucket : buckets) {
// 3. 排序桶内元素
int[] array = bucket.array();
InsertionSort.sort(array);
// System.out.println(Arrays.toString(array));
// 4. 把每个桶排序好的内容,依次放入原始数组
for (int v : array) {
ages[k++] = v;
}
}
System.out.println(Arrays.toString(ages));
}
/*
0 0,1,2
1 3,4,5
2 6,7,8
3 9
*/
public static void sort(int[] a, int range) {
int max = a[0];
int min = a[0];
for (int i = 1; i < a.length; i++) {
if (a[i] > max) {
max = a[i];
}
if (a[i] < min) {
min = a[i];
}
}
// 1. 准备桶
DynamicArray[] buckets = new DynamicArray[(max - min) / range + 1];
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new DynamicArray();
}
// 2. 放入数据
for (int age : a) {
buckets[(age - min) / range].addLast(age);
}
int k = 0;
for (DynamicArray bucket : buckets) {
// 3. 排序桶内元素
int[] array = bucket.array();
InsertionSort.sort(array);
// System.out.println(Arrays.toString(array));
// 4. 把每个桶排序好的内容,依次放入原始数组
for (int v : array) {
a[k++] = v;
}
}
}
}
10.基数排序
基数排序(Radix Sort)是一种非比较型的排序算法,它将整数按照位数切割成不同的数字,然后按每个位数进行排序。基数排序的实现可以使用计数排序或桶排序作为子排序算法。
代码:
这里考虑到字符存在
package com.dreams.sort;
import java.util.ArrayList;
/**
* 基数排序 最低有效数字 LSD(Least significant digit)
*/
public class RadixSort {
public static void radixSort(String[] a, int length) {
// 1. 准备桶
ArrayList<String>[] buckets = new ArrayList[128];
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new ArrayList<>();
}
// 2. 进行多轮按位桶排序
for (int i = length - 1; i >= 0; i--) {
// 将字符串放入合适的桶
for (String s : a) {
buckets[s.charAt(i)].add(s);
}
// 重新取出排好序的字符串,放回原始数组
int k = 0;
for (ArrayList<String> bucket : buckets) {
for (String s : bucket) {
a[k++] = s;
}
bucket.clear();
}
// System.out.println(Arrays.toString(a));
}
}
public static void main(String[] args) {
String[] phoneNumbers = new String[10]; // 0~127
phoneNumbers[0] = "13812345678"; // int long
phoneNumbers[1] = "13912345678";
phoneNumbers[2] = "13612345678";
phoneNumbers[3] = "13712345678";
phoneNumbers[4] = "13512345678";
phoneNumbers[5] = "13412345678";
phoneNumbers[6] = "15012345678";
phoneNumbers[7] = "15112345678";
phoneNumbers[8] = "15212345678";
phoneNumbers[9] = "15712345678";
/*String[] phoneNumbers = new String[6];
phoneNumbers[0] = "158";
phoneNumbers[1] = "151";
phoneNumbers[2] = "235";
phoneNumbers[3] = "138";
phoneNumbers[4] = "139";
phoneNumbers[5] = "159";*/
/*
0
1 151
2
3
4
5 135
6
7
8 158 138
9 139 159
151 135 158 138 139 159 按个位排
0
1
2
3 135 138 139
4
5 151 158 159
6
7
8
9
135 138 139 151 158 159 按十位排
*/
RadixSort.radixSort(phoneNumbers, 11);
for (String phoneNumber : phoneNumbers) {
System.out.println(phoneNumber);
}
}
}
11.java排序
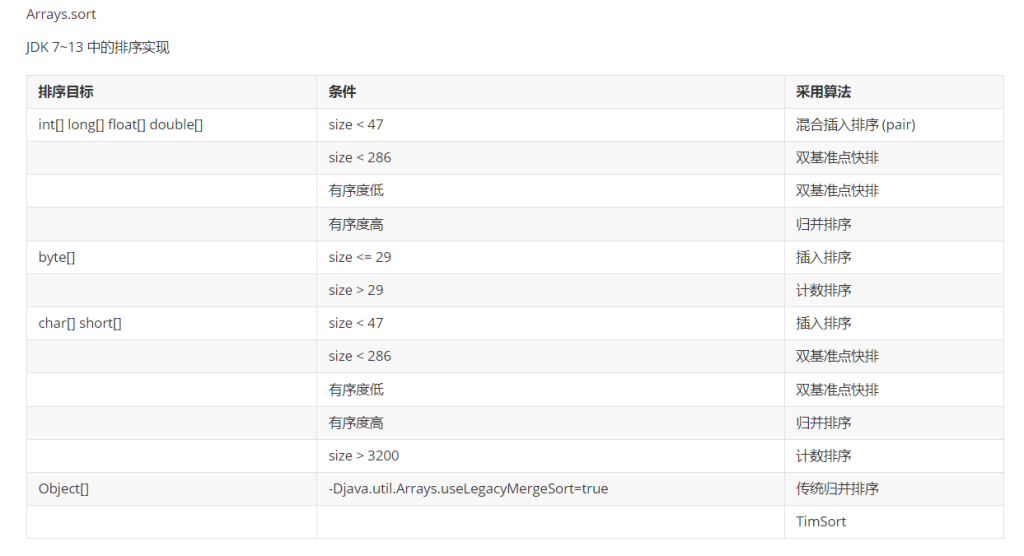
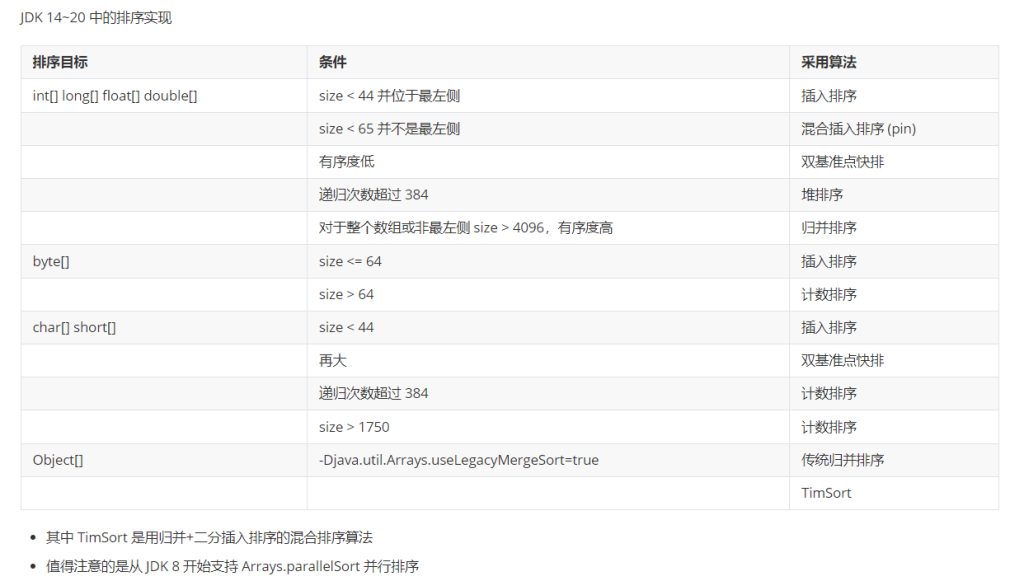
参考