1.卡特兰数规律

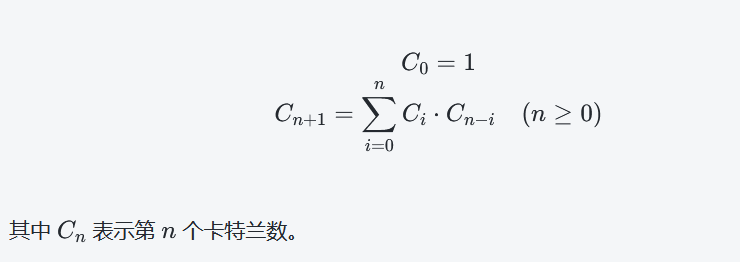
实现起来很简单：

package com.dreams.dynamicprogramming;

public class Catalan {
    public static void main(String[] args) {
        System.out.println(catalan(6));
    }

    static int catalan(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int j = 2; j < n + 1; j++) {
            for (int i = 0; i < j; i++) { // 第j个卡特兰数的拆分
                dp[j] += dp[i] * dp[j - 1 - i];
            }
        }
        return dp[n];
    }
}

2.卡特兰数应用

二叉树

这就是典型的

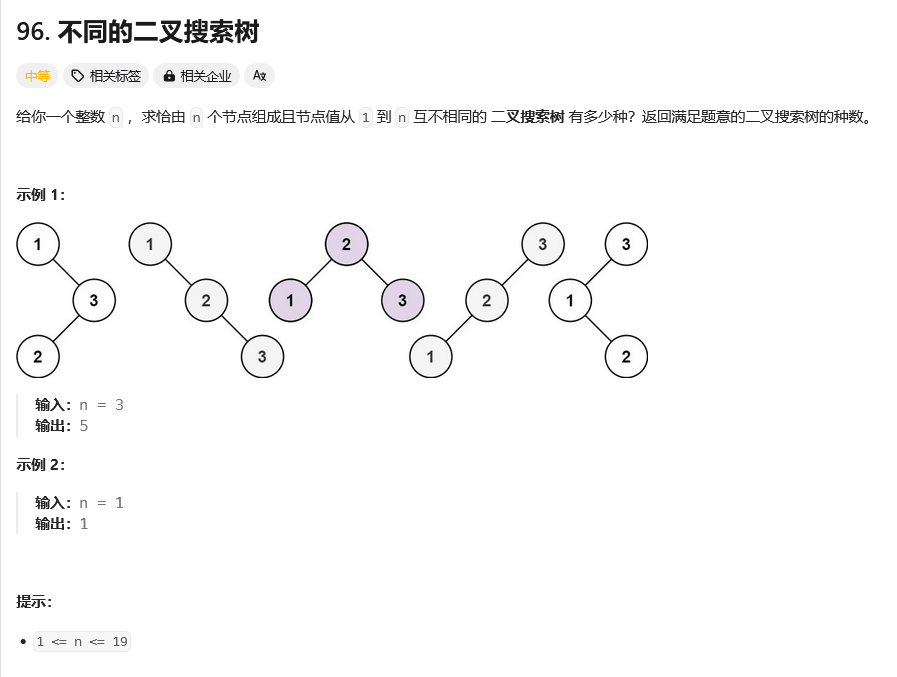
执行的效率也不错

出栈序列

n个元素进栈序列为： 1，2，3，4，…，n，则有多少种出栈序列。

同样是卡特兰数

求解方法代码同上

生成括号对数

  （）   -->      （）

                （）（）
 （）（） -->             
                （（ ））

同样是卡特兰数

package com.dreams.dynamicprogramming;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * 括号生成
 */
public class Leetcode22 {
    public List<String> generateParenthesis(int n) {
        ArrayList<String>[] dp = new ArrayList[n + 1];
        dp[0] = new ArrayList<>(Arrays.asList(""));
        dp[1] = new ArrayList<>(Arrays.asList("()"));
        for (int j = 2; j < n + 1; j++) {
            dp[j] = new ArrayList<>();
            for (int i = 0; i < j; i++) { // 第j个卡特兰数的拆分
                // i 对应的集合是内层要嵌套的括号, j - 1 - i 对应的集合是平级要拼接的括号
                //  dp[j] += dp[i] * dp[j - 1 - i];
                for (String k1 : dp[i]) {
                    for (String k2 : dp[j - 1 - i]) { // ""
                        dp[j].add("(" + k1 + ")" + k2);
                    }
                }
            }
        }
        return dp[n];
    }

    public static void main(String[] args) {
        Leetcode22 code = new Leetcode22();
        System.out.println(code.generateParenthesis(3));
    }
}

不过效率不高

参考

黑马数据结构