回溯
Dreams
|
337
|
0

1015 字
|
16 分钟

1.基本概述

回溯算法（Backtracking）是一种用于解决组合问题和搜索问题的算法。它通过在潜在的解空间中搜索，并通过试错的方式逐步找到可能的解决方案。在搜索过程中，如果发现当前路径无法继续前进，则回溯到上一步，尝试其他路径。回溯算法是一种递归算法，它通过系统地遍历可能的选项来寻找解决方案。

 

2.全排列

回溯算法生成所有可能的排列。在回溯过程中，算法会维护一个临时列表 tempList，用于存储当前生成的排列。首先判断 tempList 的大小是否等于输入数组的长度，如果是，则说明已经生成了一个排列，将其加入结果集；否则，算法遍历数组中的每个元素，如果该元素已经在 tempList 中，则跳过，否则将其加入 tempList，并继续递归调用 backtrack 方法生成下一个元素。在递归调用之后，算法会执行回溯操作，将 tempList 中的最后一个元素移除，尝试下一个可能的元素。

代码：

package com.dreams.data;

import java.util.*;

public class Permutations03 {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        backtrack(nums, new ArrayList<>(), result);
        return result;
    }
    
    private void backtrack(int[] nums, List<Integer> tempList, List<List<Integer>> result) {
        if (tempList.size() == nums.length) {
            result.add(new ArrayList<>(tempList)); // 如果临时列表的大小等于数组的长度，说明已经生成了一个排列，将其加入结果集
        } else {
            for (int i = 0; i < nums.length; i++) {
                if (tempList.contains(nums[i])) continue; // 如果临时列表中已经包含当前元素，则跳过
                tempList.add(nums[i]); // 将当前元素加入临时列表
                backtrack(nums, tempList, result); // 递归调用，继续生成下一个元素
                tempList.remove(tempList.size() - 1); // 回溯，移除最后一个元素，尝试下一个可能的元素
            }
        }
    }
    
    public static void main(String[] args) {
        Permutations03 solution = new Permutations03();
        int[] nums = {1, 2, 3};
        List<List<Integer>> result = solution.permute(nums);
        System.out.println(result);
    }


}

 

3.全排列不重复

要生成不重复的全排列，只要在上面的代码中生成每个排列时检查是否已经存在相同的排列。

为了确保排列的唯一性，先对输入数组进行排序。然后，在回溯过程中，使用一个布尔数组 used 来跟踪每个元素是否已经被使用过，并且在处理重复元素时进行了判断，以确保生成的排列是不重复的。

代码：

package com.dreams.data;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class UniquePermutations {

    public static List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums); // 先对数组进行排序，以便于后续去重
        backtrack(nums, new ArrayList<>(), new boolean[nums.length], result);
        return result;
    }

    private static void backtrack(int[] nums, List<Integer> tempList, boolean[] used, List<List<Integer>> result) {
        if (tempList.size() == nums.length) {
            result.add(new ArrayList<>(tempList));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            // user[i]来判断是否跳过重复元素，i>0判断不要超过索引
            if (used[i] || (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])) {
                continue; // 跳过重复元素
            }
            used[i] = true;
            tempList.add(nums[i]);
            backtrack(nums, tempList, used, result);
            tempList.remove(tempList.size() - 1);
            used[i] = false;
        }
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 1};
        List<List<Integer>> result = permuteUnique(nums);
        for (List<Integer> list : result) {
            System.out.println(list);
        }
    }
}

 

4.组合

需要注意的是要传递每次的i+1避免出现12的组合和21的组合重复。

package com.dreams.backtracking;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

/**
 * 组合 回溯
 */
public class Leetcode77 {
    // 此 n 代表数字范围, 1~n
    static List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> result = new ArrayList<>();
        dfs(1, n, k, new LinkedList<>(), result);
        return result;
    }

    // start 起始处理数字
    static void dfs(int start, int n, int k,
                    LinkedList<Integer> stack,
                    List<List<Integer>> result) {
        if (stack.size() == k) {
            result.add(new ArrayList<>(stack));
            return;
        }
        for (int i = start; i <= n ; i++) {
            //  还差几个数字          剩余可用数字
            if (k - stack.size() > n - i + 1) {
                continue;
            }
            stack.push(i);
            dfs(i + 1, n, k, stack, result);
            stack.pop();
        }
    }

    public static void main(String[] args) {
        List<List<Integer>> lists = combine(4, 3);
        for (List<Integer> list : lists) {
            System.out.println(list);
        }
    }
}

 

 

5.组合总和

第一反应可能是使用动态规划，组合总和问题的性质不适合动态规划，因为其无法优化子问题的重叠，在组合总和问题中，每个子问题通常都是不同的组合。因为问题的性质是要选择一定数量的数，使它们的和等于目标值，所以很难找到重叠的子问题，难以利用动态规划的优势。

代码：

package com.dreams.backtracking;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

/**
 * 组合总和 回溯
 */
public class Leetcode39 {
    static List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> result = new ArrayList<>();
        dfs(0, candidates, target, new LinkedList<>(), result);
        return result;
    }

    static void dfs(int start, int[] candidates, int target, LinkedList<Integer> stack, List<List<Integer>> result) {
        if (target == 0) {
            result.add(new ArrayList<>(stack));
            return;
        }
        for (int i = start; i < candidates.length; i++) {
            int candidate = candidates[i];
            if (target < candidate) {
                continue;
            }
            stack.push(candidate);
            dfs(i, candidates, target - candidate, stack, result);
            stack.pop();
        }
    }

    public static void main(String[] args) {
        List<List<Integer>> lists = combinationSum(new int[]{2, 3, 6, 7}, 7);
        for (List<Integer> list : lists) {
            System.out.println(list);
        }
    }
}

 

 

6.组合总和II

与上一题不同的就是candidates 中的每个数字在每个组合中只能使用一次。

只要start加一传递递归就行，然后参考全排列不重复，添加属性

代码：

package com.dreams.backtracking;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;

/**
 * 组合总和 II 回溯
 */
public class Leetcode40 {
    static List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(candidates);
        System.out.println(Arrays.toString(candidates));
        dfs(0, candidates, new boolean[candidates.length], target, new LinkedList<>(), result);
        return result;
    }

    static void dfs(int start, int[] candidates, boolean[] visited, int target, LinkedList<Integer> stack, List<List<Integer>> result) {
        if (target == 0) {
            result.add(new ArrayList<>(stack));
            return;
        }
        for (int i = start; i < candidates.length; i++) {
            int candidate = candidates[i];
            if (target < candidate) {
                continue;
            }
            if (i > 0 && candidate == candidates[i - 1] && !visited[i - 1]) {
                continue;
            }
            visited[i] = true;
            stack.push(candidate);
            dfs(i + 1, candidates, visited, target - candidate, stack, result);
            stack.pop();
            visited[i] = false;
        }
    }

    public static void main(String[] args) {
        int[] candidates = {10, 1, 2, 7, 6, 1, 5};
        List<List<Integer>> lists = combinationSum2(candidates, 8);
        for (List<Integer> list : lists) {
            System.out.println(list);
        }
    }
}

可以看到，回溯要求不重复，通常是先排序再插传入start+1。

 

7.组合总和III

这里和回溯的组合对比，注意一下减枝条件。

if(target < i){
    continue;
}
if(stack.size() == k) {
    continue;
}

代码：

package com.dreams.backtracking;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

/**
 * 组合总和 III 回溯
 */
public class Leetcode216 {
    // 此 target 代表数字组合后的和
    static List<List<Integer>> combinationSum3(int k, int target) {
        List<List<Integer>> result = new ArrayList<>();
        dfs(1, target, k, new LinkedList<>(), result);
        return result;
    }

    static void dfs(int start, int target, int k,
                    LinkedList<Integer> stack,
                    List<List<Integer>> result) {
        if (target == 0 && stack.size() == k) {
            result.add(new ArrayList<>(stack));
            return;
        }
        for (int i = start; i <= 9; i++) {
            if(target < i){
                continue;
            }
            if(stack.size() == k) {
                continue;
            }
            stack.push(i);
            dfs(i + 1, target - i, k, stack, result);
            stack.pop();
        }
    }

    public static void main(String[] args) {
        List<List<Integer>> lists = combinationSum3(2, 18); // 9 8
        for (List<Integer> list : lists) {
            System.out.println(list);
        }
    }
}

 

 

8.N皇后

冲突：

  • 列冲突：使用一个boolean数组ca来记录每一列是否已经放置了皇后。当放置皇后时，如果该列已经有皇后存在，则发生冲突。
  • 左斜线冲突：对于左斜线上的冲突，可以使用一个boolean数组cb来记录。左斜线上的每个位置的行号与列号之和是一个常数，通过这个特性可以判断是否发生冲突。
  • 右斜线冲突：右斜线上的每个位置的行号与列号之差也是一个常数，可以利用这一特性来判断是否发生冲突，使用一个boolean数组cc来记录。

代码：

package com.dreams.backtracking;

import java.util.Arrays;

/**
 * N皇后 - 回溯
 */
public class Leetcode51 {
    public static void main(String[] args) {
        int n = 4;
        boolean[] ca = new boolean[n]; // 记录列冲突
        boolean[] cb = new boolean[2 * n - 1]; // 左斜线冲突
        boolean[] cc = new boolean[2 * n - 1]; // 右斜线冲突
        char[][] table = new char[n][n]; // '.' 'Q'
        for (char[] t : table) {
            Arrays.fill(t, '.');
        }
        dfs(0, n, table, ca, cb, cc);
    }

    static void dfs(int i, int n, char[][] table, boolean[] ca, boolean[] cb, boolean[] cc) {
        if (i == n) { // 找到解
            System.out.println("-------------------");
            for (char[] t : table) {
                System.out.println(new String(t));
            }
            return;
        }
        for (int j = 0; j < n; j++) {
            if (ca[j] || cb[i + j] || cc[n - 1 - (i - j)]) {
                continue;
            }
            table[i][j] = 'Q';
            ca[j] = cb[i + j] = cc[n - 1 - (i - j)] = true;
            dfs(i + 1, n, table, ca, cb, cc);
            table[i][j] = '.';
            ca[j] = cb[i + j] = cc[n - 1 - (i - j)] = false;
        }
    }
}

 

9.解数独

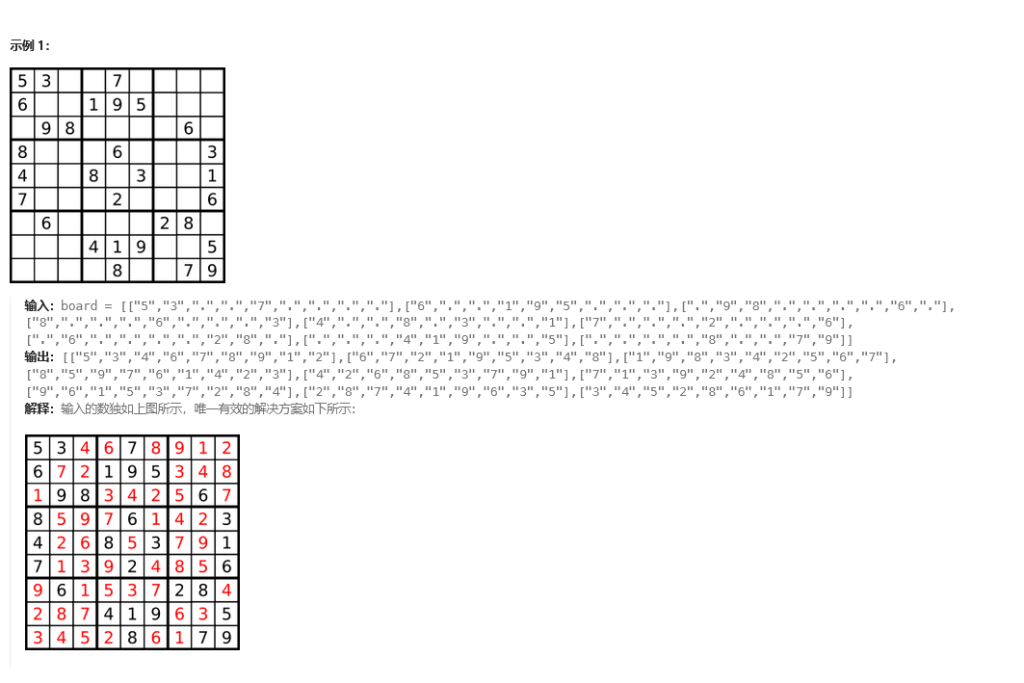
判断在哪个九宫格只要i/3*3+j/3就可以知道在哪里

代码：

package com.dreams.backtracking;

import java.util.Arrays;

public class Leetcode37 {

    static void solveSudoku(char[][] table) {
        /*
            1. 不断遍历每个未填的空格
               逐一尝试 1~9 若行、列、九宫格内没有冲突，则填入
            2. 一旦 1~9 都尝试失败，回溯到上一次状态，换数字填入
            3. 关键还是要记录冲突状态
         */
        // 行冲突状态
        boolean[][] ca = new boolean[9][9];
        // ca[i] = {false,false,true,true,true,true,true,true,true}
        // 列冲突状态
        boolean[][] cb = new boolean[9][9];
        // cb[j] = {false,true,true,false,true,true,true,true,false}
        // 九宫格冲突状态
        // i/3*3+j/3
        boolean[][] cc = new boolean[9][9];
        // cc[i/3*3+j/3] = {true,false,true,true,true,true,false,true,true}
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                char ch = table[i][j];
                if (ch != '.') { // 初始化冲突状态
                    ca[i][ch - '1'] = true;   // '5' - '1' -> 4
                    cb[j][ch - '1'] = true;
                    cc[i / 3 * 3 + j / 3][ch - '1'] = true;
                }
            }
        }
        dfs(0, 0, table, ca, cb, cc);
    }

    static boolean dfs(int i, int j, char[][] table, boolean[][] ca, boolean[][] cb, boolean[][] cc) {
        while (table[i][j] != '.') { // 查找下一个空格
            if (++j >= 9) {
                j = 0;
                i++;
            }
            if (i >= 9) {
                return true; // 找到解
            }
        }
        for (int x = 1; x <= 9; x++) {
            // 检查冲突
            if (ca[i][x - 1] || cb[j][x - 1] || cc[i / 3 * 3 + j / 3][x - 1]) {
                continue;
            }
            // 填入数字
            table[i][j] = (char) (x + '0');  // 1 + '0' => '1'
            // ca[0][0] = true  第0行不能存储'1'
            // cb[2][0] = true  第2列不能存储'1'
            // cc[0][0] = true  第0个九宫格不能存储'1'
            // 记录填入数字后的冲突
            ca[i][x - 1] = cb[j][x - 1] = cc[i / 3 * 3 + j / 3][x - 1] = true;
            if (dfs(i, j, table, ca, cb, cc)) {
                return true;
            }
            table[i][j] = '.';
            ca[i][x - 1] = cb[j][x - 1] = cc[i / 3 * 3 + j / 3][x - 1] = false;
        }
        return false;
    }

    public static void main(String[] args) {
        char[][] table = {
                {'5', '3', '.', '.', '7', '.', '.', '.', '.'},
                {'6', '.', '.', '1', '9', '5', '.', '.', '.'},
                {'.', '9', '8', '.', '.', '.', '.', '6', '.'},
                {'8', '.', '.', '.', '6', '.', '.', '.', '3'},
                {'4', '.', '.', '8', '.', '3', '.', '.', '1'},
                {'7', '.', '.', '.', '2', '.', '.', '.', '6'},
                {'.', '6', '.', '.', '.', '.', '2', '8', '.'},
                {'.', '.', '.', '4', '1', '9', '.', '.', '5'},
                {'.', '.', '.', '.', '8', '.', '.', '7', '9'}
        };
        solveSudoku(table);

        print(table);
    }

    static char[][] solved = {
            {'5', '3', '4', '6', '7', '8', '9', '1', '2'},
            {'6', '7', '2', '1', '9', '5', '3', '4', '8'},
            {'1', '9', '8', '3', '4', '2', '5', '6', '7'},
            {'8', '5', '9', '7', '6', '1', '4', '2', '3'},
            {'4', '2', '6', '8', '5', '3', '7', '9', '1'},
            {'7', '1', '3', '9', '2', '4', '8', '5', '6'},
            {'9', '6', '1', '5', '3', '7', '2', '8', '4'},
            {'2', '8', '7', '4', '1', '9', '6', '3', '5'},
            {'3', '4', '5', '2', '8', '6', '1', '7', '9'}
    };

    static void print(char[][] table) {
        for (char[] chars : table) {
            System.out.println(new String(chars));
        }
        System.out.println(Arrays.deepEquals(table, solved));
    }
}

 

 

 

参考

黑马数据结构

暂无评论

发送评论 编辑评论

 
 
 
 
 
   
 
  
  
   
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
颜文字
Emoji
小恐龙
花!
  
上一篇
下一篇 
  推荐文章
解决/A/:id 跳转到另一个/A/:id
 
git无法提交大文件
 
CSRF引起整合 SpringSecurity 发送POST请求出现 403